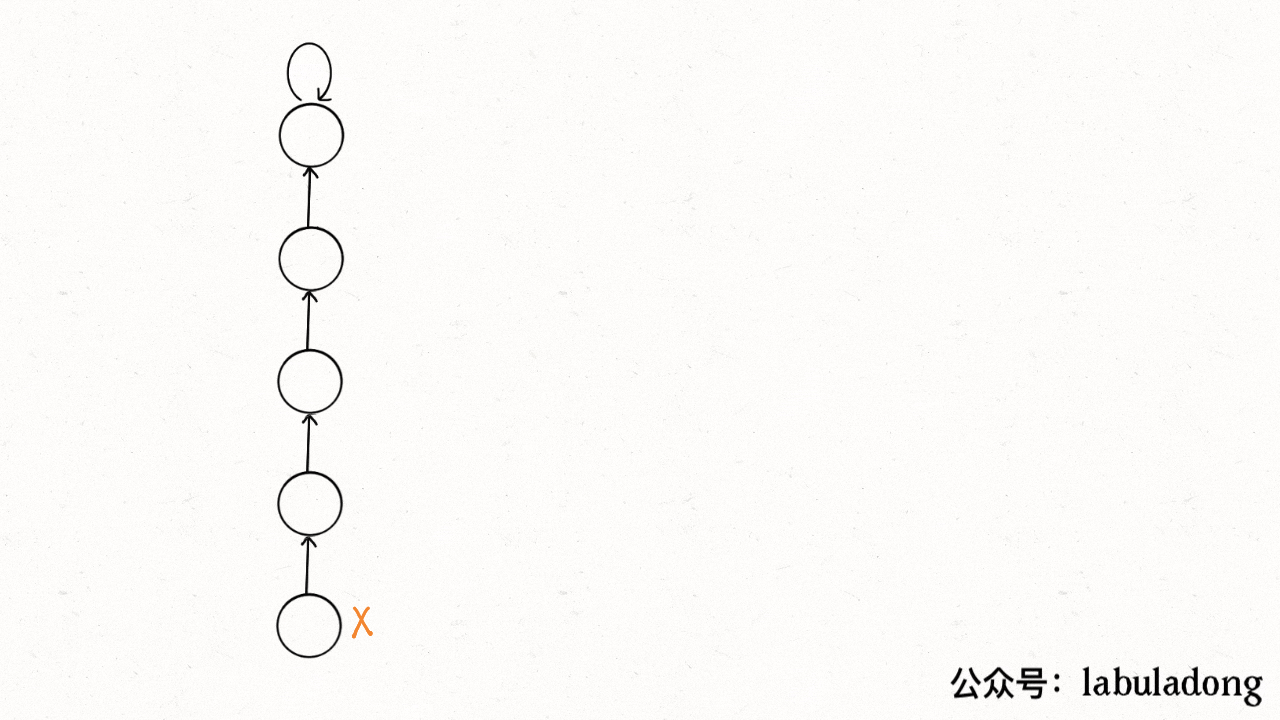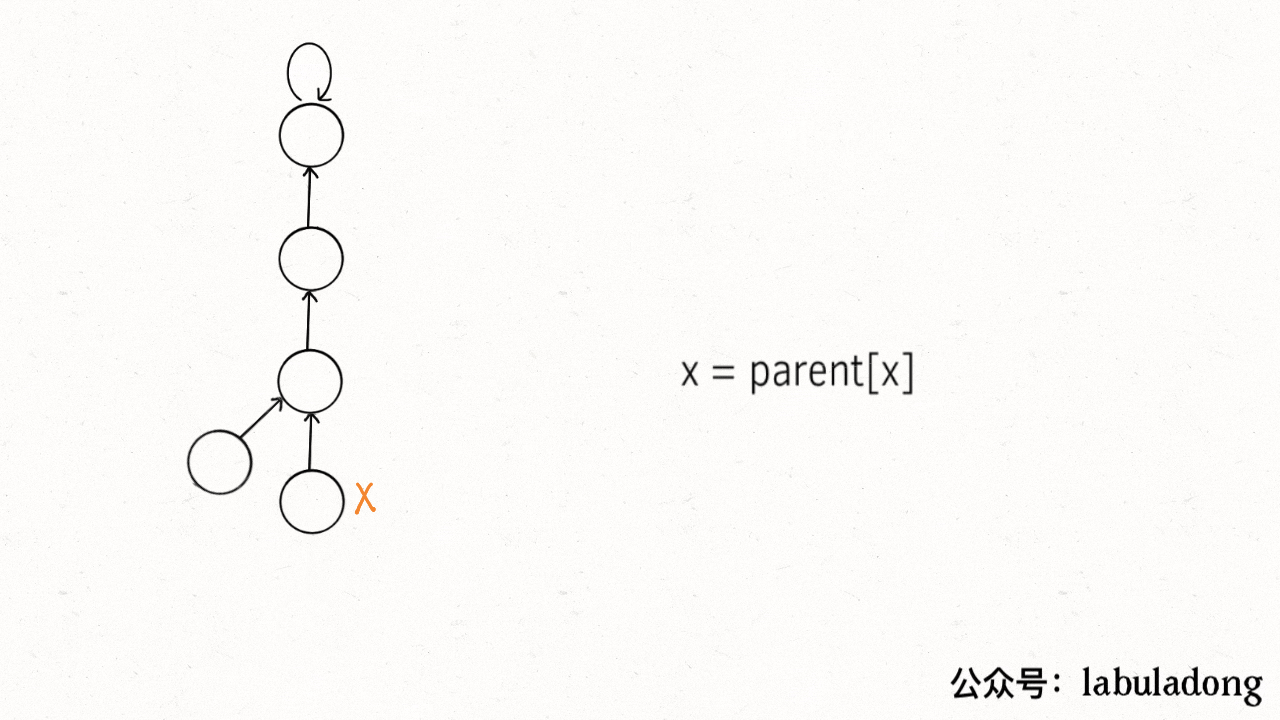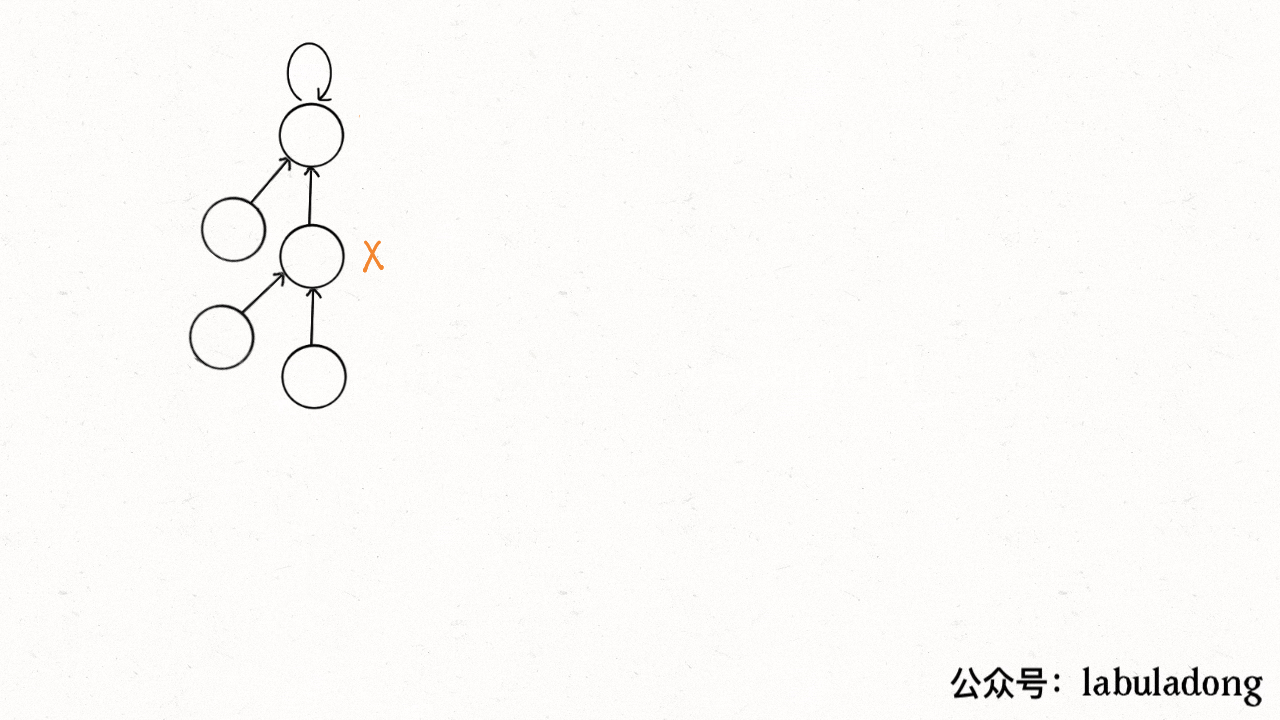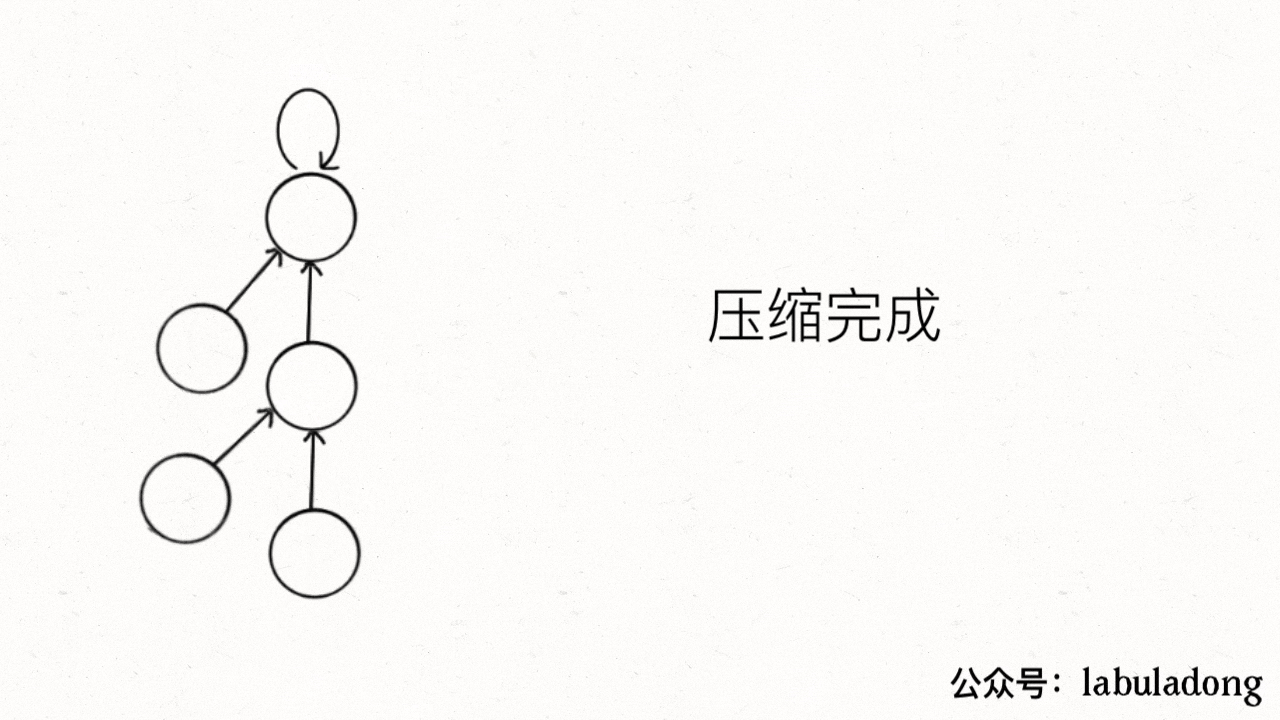并查集

并查集（UNION-FIND）

并查集（Union-Find Set）是一种用来管理和解决集合分组问题的数据结构，它支持两个操作：

• 查找（Find）：查找一个元素属于哪个集合，即找出其所在的连通块。
• 合并（Union）：将两个不相交的集合合并成一个新的集合。

并查集模板

查找（Find）：这里用树来表示是否属于同一个数组，使用查找（Find）操作返回的是该节点所在树的根节点，如果一个节点x所在树的根节点就是x自己，那么findParent(x)返回的结果就是x。

合并（Union）：合并两个节点x和y之前需要先判断x和y是否属于一个集合，如果已经在一个集合里，那么直接返回，否则将x和y的集合合并（在此实现为将x和y的树合并为一个树）。

合并两个集合最原始的方式就是将一个节点的根节点接到另一个节点的根节点上：

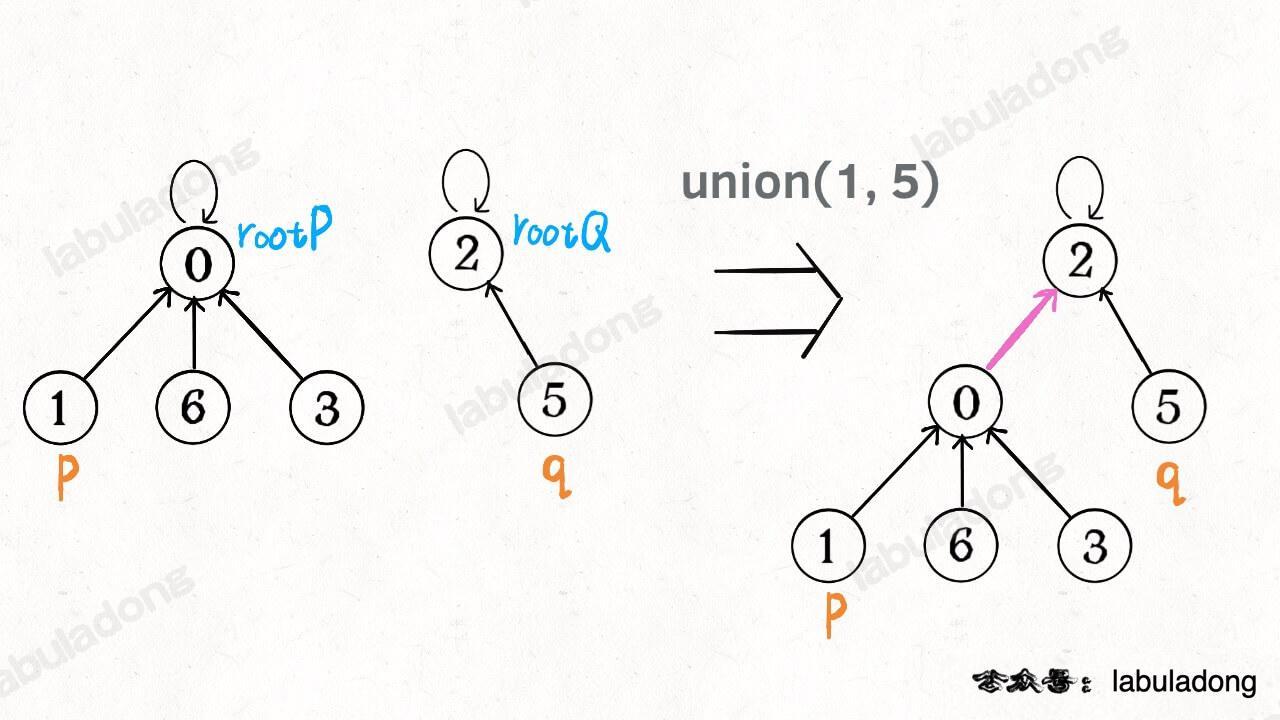
其实就是一个树结构，每个节点的祖先节点是其所在的集合，那么就会有一个问题，在最坏的情况下，树会退化为一个链表，这时候的查找时间复杂度为O(N)，上面的findParent函数可以在查找过程中将树结构进行压缩，压缩之后的结构如下图所示，每个节点的父亲节点为所在树的根节点：

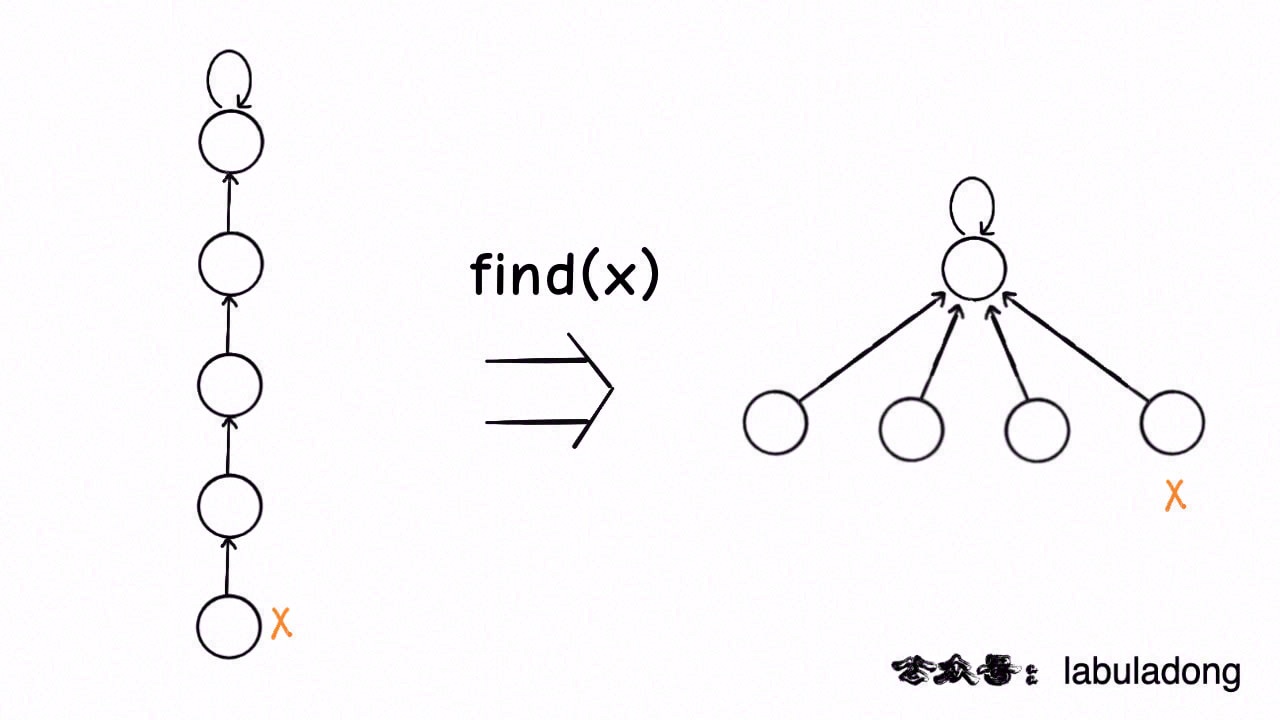
代码如下：

int findParent(int x)
{
    if(x != parent[x])
        return findParent(parent[x]);
    return parent[x];
}

其查找过程便是压缩过程，见下面的动图：

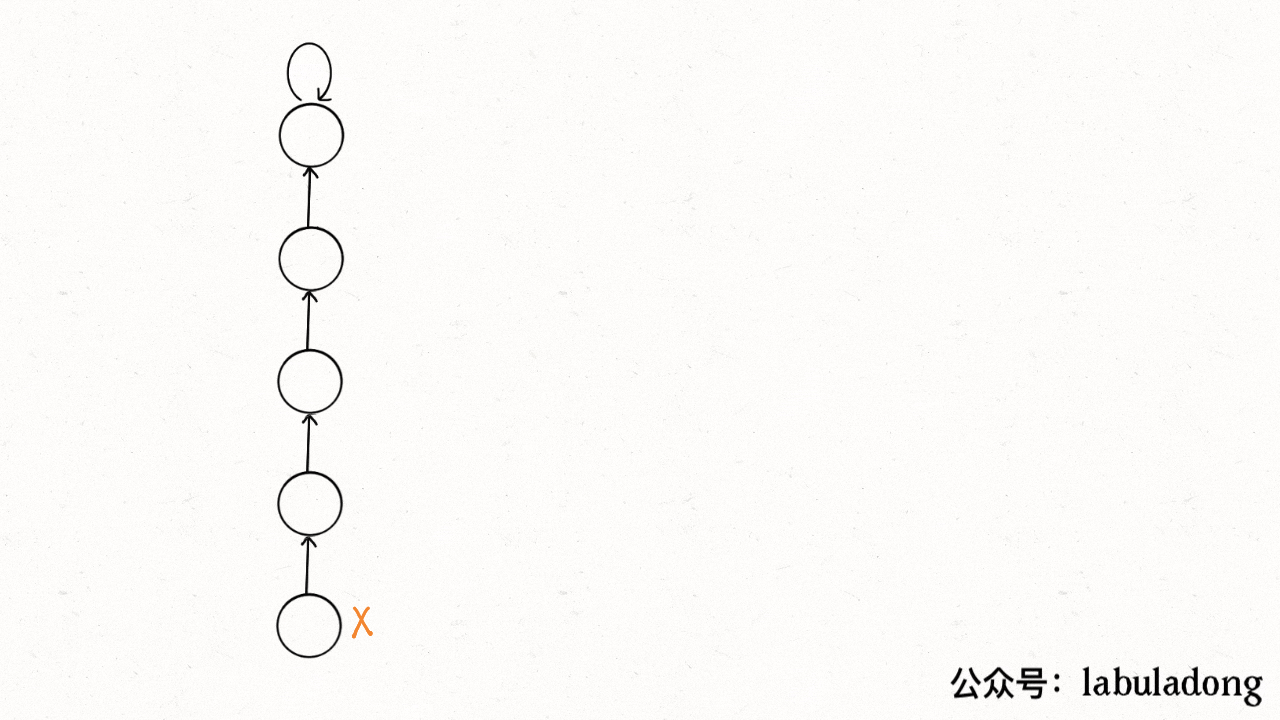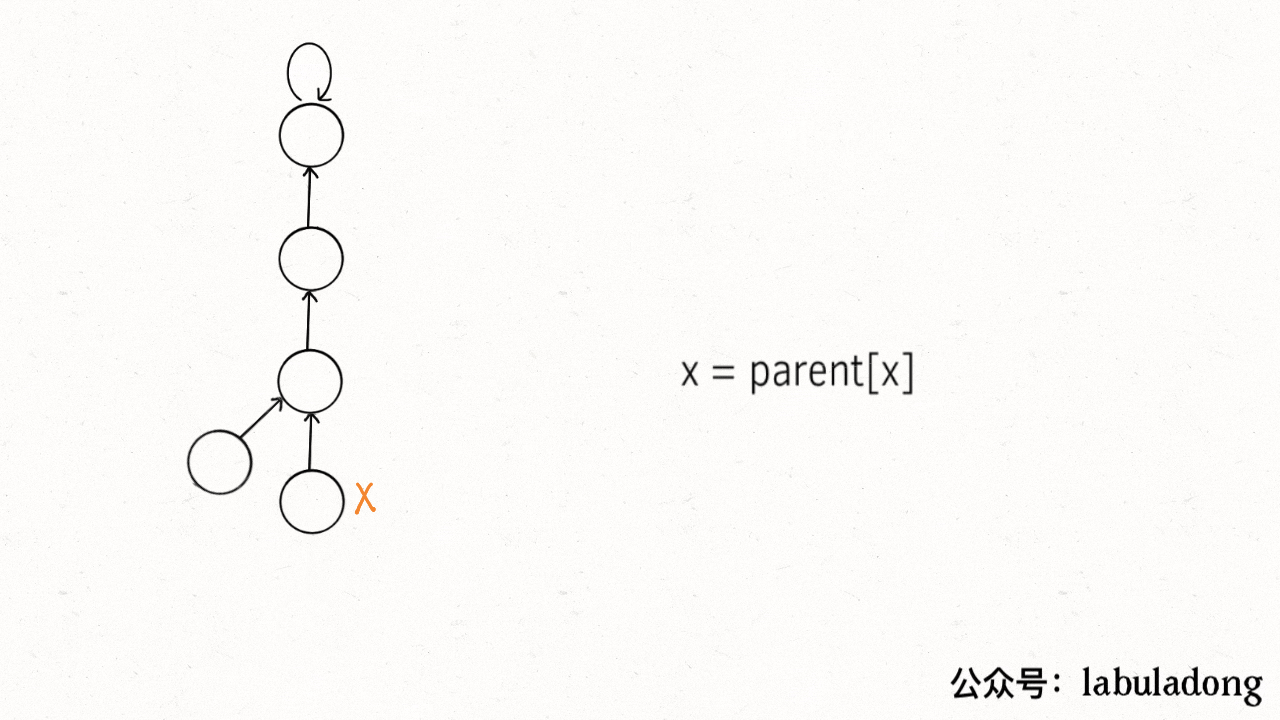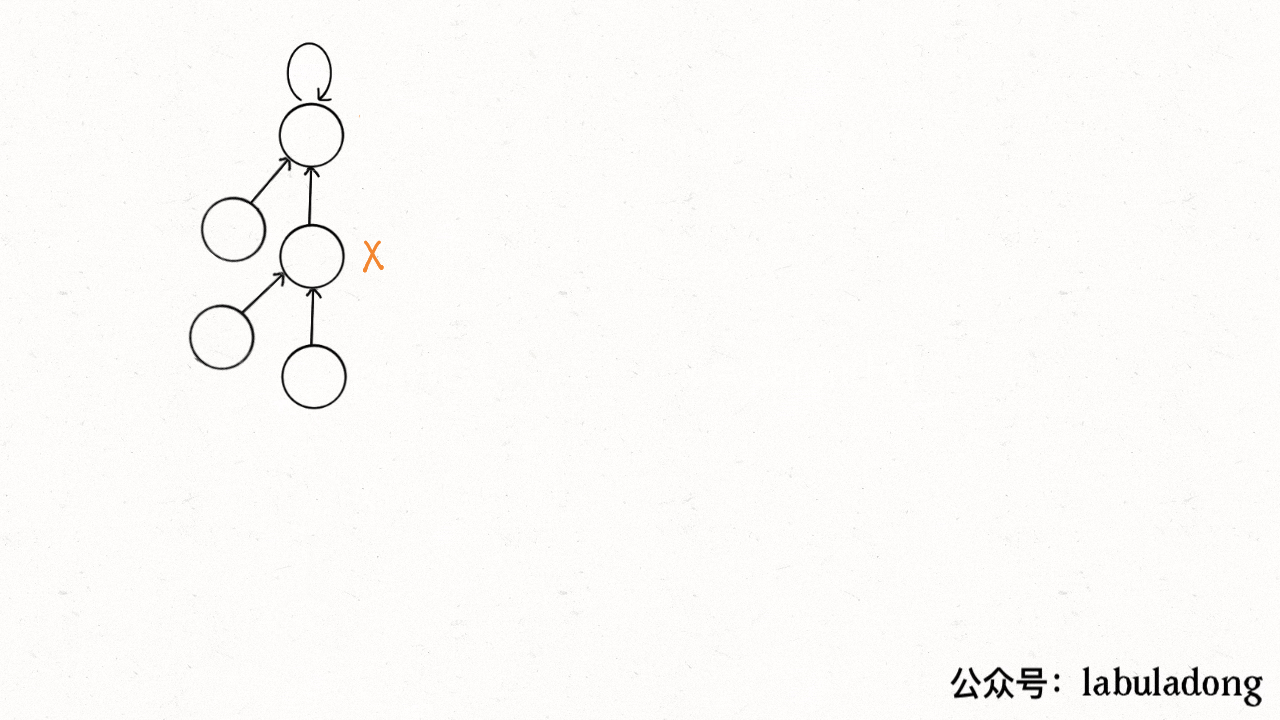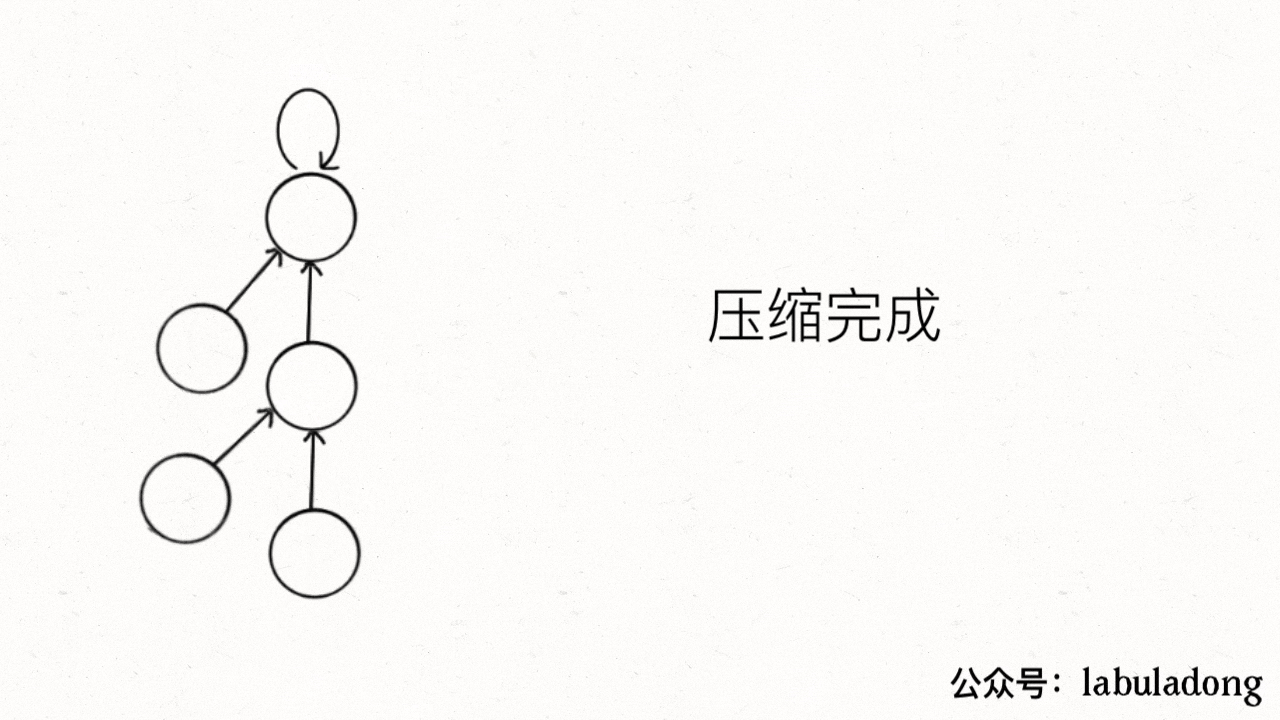
并查集的模板如下所示：

class UF
{
public:
    UF(int n)   // 构造函数，输入n为节点个数
    {
        parent = vector<int>(n);    // n + 1是可以parent[i]为第i个节点的祖先，视情况而定
        for(int i = 0; i < n; ++i)
            parent[i] = i;      // 初始时每个节点都是单独的结合
        count = n;
    }

    int findParent(int x)
    {
        if(x != parent[x])      // 路径压缩
            parent[x] = findParent(parent[x]);
        return parent[x];
    }

    void connect(int x, int y)
    {
        int parent_x = findParent(x);
        int parent_y = findParent(y);

        if(parent_x == parent_y)  // x，y已经属于同一个集合，直接返回     
            return ;
        --count;
        parent[parent_y] = parent_x;   // 将两个集合合并
    }

    bool isConnected(int x, int y)  // 判断两个节点是否属于一个集合
    {
        return findParent(x) == findParent(y);
    }

    int getCount()
    {
        return count;
    }
private:
    vector<int> parent;     // parent[i]为第i个节点的祖先
    int count;
};

参考：本文中的图引用自labuladong 的算法小抄,模板实现是根据其模板修改而来。