位运算的妙用

异或运算实现变量交换

异或运算可以理解为无进位相加，异或运算的性质如下：

• 0 ^ N = N
• N ^ N = N
• a ^ b = b ^ a (交换律)
• a ^ b ^ c = a ^ (b ^ c) （结合律）

异或运算的妙用：交换两个数的值不使用额外变量：

int a = 17, b = 23;
// 交换a，b的值
a = a ^ b;
b = a ^ b;
a = a ^ b;

但是需要注意的是，可以这样使用的前提是a和b指向的内存是不同的，但是两个数的值可以相同。 比如在一个数组中对nums[i]和nums[j]进行交换，要使用这种方法，必须要保证i和j相同，否则nums[i]位置上的数会被抹成0。所以一般情况下不推荐这种用法。

异或运算查找出现奇数次的数

只有一种数出现奇数次

一个数组中只有一种数出现奇数次，其余的数都出现偶数次，那么如果寻找这个出现奇数次的数？

设置一个\(eor = 0\),然后让\(eor\)与数组中的每个数都异或一遍，最后得到的\(eor\)就是出现奇数次的数。因为异或运算满足交换律，出现偶数次的数相互异或的结果为\(0\)，出现奇数次的数相互异或的结果为这个数的值，所以总的结果就是这个出现奇数次的数。

有两种数出现奇数次

一个数组中有两种数出现奇数次，其余的数都出现偶数次，那么如果寻找出现奇数次的数？

设置一个\(eor = 0\),然后让\(eor\)与数组中的每个数都异或一遍，最后得到的\(eor\)为a ^ b。因为a和b是不同的数，所以必然有a ^ b \(\ne\) 0,也就是a ^ b的二进制至少有一位是1，那么假设a ^ b的二进制第8位为1，让\(eor\)与数组中第8位为1的数异或，得到的\(eor^{'}\)就是a或b，再用\(eor^{'}\)与\(eor\)异或得到的就是另外一个数。

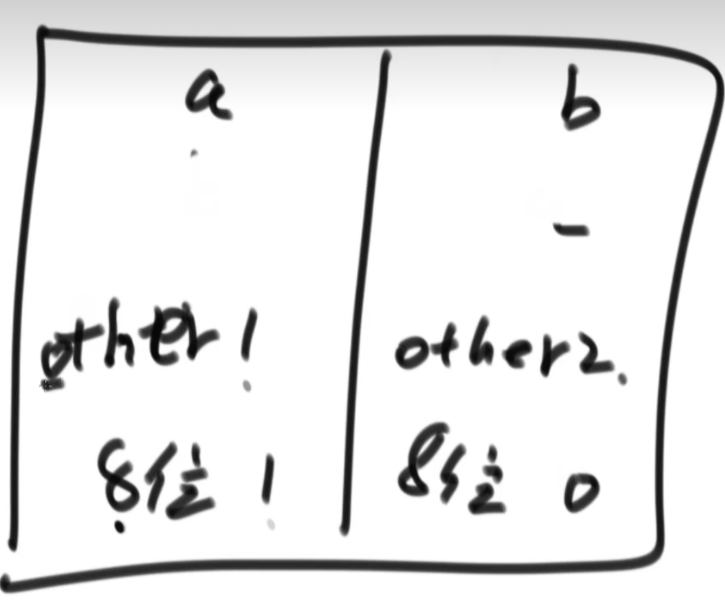
因为a和b在第8为上的值一定是不一样的，所以肯定在不同的区域里，这样去用\(eor\)异或第8位为1的数得到的就是a，b其中之一，出现偶数次的数不影响异或的结果。

那么就有一个问题，选哪一位的1？如何提取出这一位上的1？这里选择提取出a ^ b最右边一位的1。

int rightOne = eor & (~eor + 1) // 提取出eor最右侧的1

将\(eor\)用二进制表示就可以更直观的看出来：

             eor = 11001110    
        ~eor + 1 = 00110010
eor & (~eor + 1) = 00000010 // 提取出来最右侧的1

&运算消去二进制最低位的1

n & (n - 1)

因为

    n = 11001110
n - 1 = 11001101

可以看到n的二进制中的高位的\(1\)其实是不受减一操作的影响的，所以n & (n - 1)就可以在不影响其他二进制位的情况下消去其最低位的\(1\)。

那么就可以根据这个特性计算k的二进制1的个数：

int count = 0;
while(n)
{
    n &= n - 1;    // 每次消去二进制中最低位的1
    count++;
}

求两个数的均值

一般的写法是

int mid = (low + high) / 2;

但是这样并不是无懈可击的，可能会出现一个问题，当low和high都很大的时候low + high可能会溢出，这样结果就变成一个负数。更加好的写法是

int mid = low + (high - low) / 2; 

low和high都没有溢出，那么high - low也不会溢出，这样结果就不会溢出。

更加简化的写法是

int mid = low + ((high - low) >> 2);