二叉树

什么是二叉树

二叉树是一种常见的数据结构，它是每个节点至多有两棵子树的树。

二叉树有两种特殊的形式，满二叉树和完全二叉树。

满⼆叉树：如果⼀棵⼆叉树只有度为0的结点和度为2的结点，并且度为0的结点在同⼀层上，则这棵⼆叉树为满⼆叉树。一棵深度为k的满二叉树节点个数为\(2^k -1\)。

完全⼆叉树：至多只有最下面的两层结点的度数可以小于2, 并且最下一层上的结点都集中在该层最左边的若干位置上， 则此二叉树称为完全二叉树。

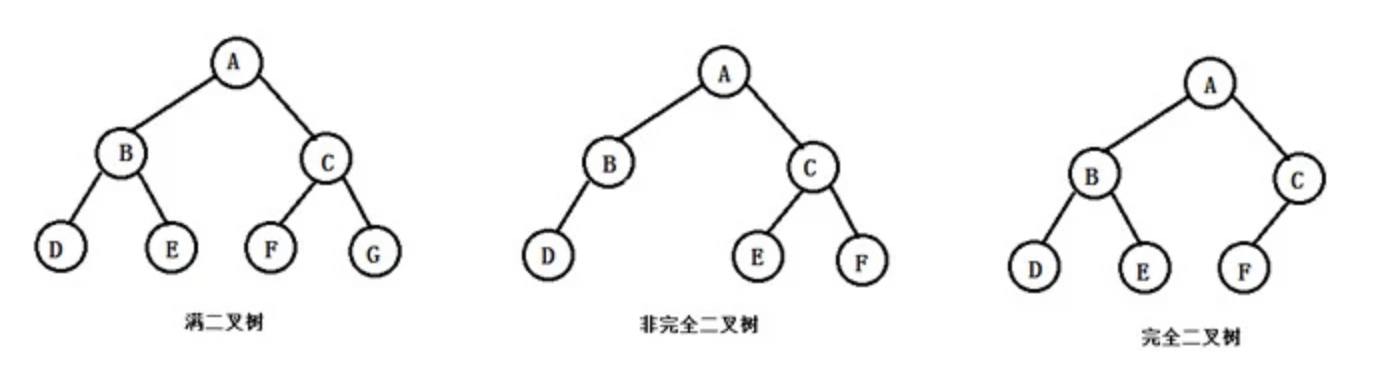
我们可以看出满二叉树是完全二叉树， 但完全二叉树不一定是满二叉树。

二叉搜索树（二叉排序树）

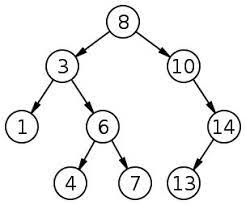
二叉排序树虽然名叫排序树，但是它其实是用来搜索的，是一种有序的二叉树。它遵循着左小右大的规则：

• 若它的左⼦树不空，则左⼦树上所有结点的值均⼩于它的根结点的值；
• 若它的右⼦树不空，则右⼦树上所有结点的值均⼤于它的根结点的值；
• 它的左、右⼦树也分别为⼆叉搜索树。

平衡二叉树

二叉搜索树有一个缺点，在插入数据是有序的序列（包括升序和降序），会导致二叉树退化成链表，从而导致在查找，删除，添加时的性能均从O（logN）降低为O（N），这是不能接受的。

究其原因，是因为二叉搜索树退化成链表的时候，树的高度与节点的个数相等，也就是成正比，所以为了优化这种情况，就出现了具有平衡能力的二叉搜索树，其中AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O（logN）。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。

平衡二叉树的性质

平衡二叉树本质上是特殊的二叉搜索树（二叉排序树），它具有二叉搜索树所有的特点，此外它有自己的特别的性质，如下：

• 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1；
• 平衡二叉树的左右两个子树都是一棵平衡二叉树。

平衡因子指的是，平衡二叉树在保持平衡的时候，是通过平衡因子来判断的

\[节点的平衡因子 = 该节点的左子树的高度 - 该节点右子树的高度\]

只有当值等于-1（右子树的高度大），0（左右子树的高度相等），1（左子树的高度大）的时候，能够代表该子树是平衡的除此之外，就认为该节点已经失衡了，需要旋转来维持平衡。

二叉树的遍历

二叉树的遍历是对于理解二叉树以及应对二叉树问题必不可少的因素，甚至有很多算法问题都是基于二叉树的不同遍历算法来做的。

二叉树的遍历有多种实现方式，不同的方式这里都要熟练掌握，只有熟练掌握不同的遍历方式才能以不变应万变来应对不同的问题。

递归法

很简单，不需要多说，二叉树的前序、中序、后序遍历其实都是一个模板，区别在于它们将当前节点值添加到结果数组res的时间不一样，而这种区别是由不同遍历方式下父节点与子节点的遍历次序导致的。

前序遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
vector<int> inorderTraversal(TreeNode* root)
{
    vector<int> res;
    oreOrder(root, res);
    return res;
}

void preOrder(TreeNode *root, vector<int> &res)
{
    if(root == nullptr)
        return ;
    res.emplace_back(res -> val, res);
    preOrder(root -> left);
    preOrder(root -> right, res);
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

中序遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

vector<int> inorderTraversal(TreeNode* root)
{
    vector<int> res;
    inOrder(root, res);
    return res;
}

void inOrder(TreeNode* root, vector<int> &res)
{
    if(root == nullptr)
        return ;
    inOrder(root -> left, res);
    res.emplace_back(root -> val);
    inOrder(root -> right, res);
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

后序遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
vector<int> postorderTraversal(TreeNode* root)
{
    vector<int> res;
    postOrder(root, res);
    return res;
}

void postOrder(TreeNode* root, vector<int> &res)
{ 
    if(root == nullptr)
        return ;
    postOrder(root -> left, res);
    postOrder(root -> right, res);
    res.emplace_back(root -> val);
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

迭代法

前序遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
vector<int> preorderTraversal(TreeNode* root)
{
    vector<int> res;
    if(root == nullptr)
        return res;
    stack<TreeNode*> stk;
    TreeNode* cur = root;
    while(!stk.empty() || cur != nullptr)
    {
        while(cur != nullptr)
        {
            res.emplace_back(cur -> val);
            stk.emplace(cur);
            cur = cur -> left;
        }
        cur = stk.top();
        stk.pop();
        cur = cur -> right;
    }
    return res;
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

中序遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
vector<int> inorderTraversal(TreeNode* root)
{
    vector<int> res;
    if(root == nullptr)
        return res;
    TreeNode* cur = root;
    stack<TreeNode*> stk;
    while(!stk.empty() || cur != nullptr)
    {
        while(cur != nullptr)
        {
            stk.emplace(cur);
            cur = cur -> left;
        }
        cur = stk.top();
        stk.pop();
        res.emplace_back(cur -> val);
        cur = cur -> right;
    }
    return res;
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

后序遍历

迭代法的后序遍历相比较前序遍历和中序遍历是要麻烦一些的。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
vector<int> postorderTraversal(TreeNode* root) 
{
    vector<int> res;
    if(root == nullptr)
        return res;
    stack<TreeNode*> stk;
    TreeNode* cur = root, * pre = nullptr;
    // stk.emplace(cur);
    while(!stk.empty() || cur != nullptr)
    {
        while(cur != nullptr)
        {
            stk.emplace(cur);
            cur = cur -> left;
        }
        cur = stk.top();
        stk.pop();
        if(cur -> right != nullptr && cur -> right != pre)
        {
            stk.emplace(cur);   // 若右孩子存在且没有遍历过那么将cur重新压栈，访问右子树
            cur = cur -> right;
        }
        else
        {
            res.emplace_back(cur -> val);
            pre = cur;
            cur = nullptr;
        }
    }
    return res;
    
    
}

复杂度分析：

• 时间复杂度：\(O(n)\),其中 \(n\) 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：\(O(n)\)，为迭代过程中显式栈的开销，平均情况下为 \(O(\log n)\)，最坏情况下树呈现链状，为 \(O(n)\)。

Morris法

Morris法只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

前序遍历

Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其前序遍历规则总结如下（假设当前遍历到的节点为 cur）:

1. 如果cur的左子节点为空，将cur加入答案，并遍历cur的右子节点；
2. 如果cur的左子节点不为空，在cur的左子树中找到cur在中序遍历下的前驱节点：
   • 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为cur,然后将cur加入答案。cur更新为cur的左子节点。
   • 如果前驱节点的右子节点不空，也就是前驱节点的右子节点为cur，说明我们已经遍历完 cur 的左子树。cur更新为cur的右子节点。
3. 重复步骤 1 和步骤 2，直到遍历结束。

这样我们利用 Morris 遍历的方法，前序遍历该二叉树，即可实现线性时间与常数空间的遍历。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 vector<int> preorderTraversal(TreeNode* root)
 {
    vector<int> res;
    if(root == nullptr)
        return res;
    TreeNode* cur = root, * pre;
    while(cur != nullptr)
    {
        pre = cur -> left;
        if(pre == nullptr)      // 左子节点为空直接将val加入res中
        {
            res.emplace_back(cur -> val);
        }
        else        // 左子节点不为空寻找cur的前驱节点
        {
            while(pre -> right != nullptr && pre -> right != cur)
                pre = pre -> right;
            if(pre -> right == nullptr) // 前驱节点右指针为空说明还没有遍历过cur的左子树
            {
                res.emplace_back(cur -> val);
                pre -> right = cur;
                cur = cur -> left;
                continue;
            }  
            else        // 否则说明已经遍历过cur的左子树，将前驱节点右指针重新设置为空
            {
                pre -> right = nullptr;
            }
        }
        cur = cur -> right;
    }
    return res;
 }

复杂度分析：

• 时间复杂度：\(O(n)\)，其中 \(n\) 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
• 空间复杂度：\(O(1)\)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

中序遍历

Morris法的中序遍历与前序遍历的思想是相同的，不同的是在当前节点的左孩子存在时的处理方式不同，思路如下（假设当前遍历到的节点为 cur）：

1. 如果cur的左子节点为空，将cur加入答案，并遍历cur的右子节点；
2. 如果cur的左子节点不为空，在cur的左子树中找到cur在中序遍历下的前驱节点：
   • 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为cur。cur更新为cur的左子节点。
   • 如果前驱节点的右子节点不空，也就是前驱节点的右子节点为cur，说明我们已经遍历完 cur 的左子树，将它的右子节点重新设为空，然后将当cur加入答案。然后将cur更新为cur的右子节点。
3. 重复步骤 1 和步骤 2，直到遍历结束。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 vector<int> inorderTraversal(TreeNode* root)
 {
    vector<int> res;
    if(root == nullptr)
        return res;
    TreeNode* cur = root,* pre = nullptr;
    while(cur != nullptr)
    {
        if(cur -> left == nullptr)  // 左子节点为空直接遍历右子树
        {
            res.emplace_back(cur -> val);
            cur = cur -> right;
        }
        else    // 左子节点不为空寻找cur的前驱节点
        {
            pre = cur -> left;
            while(pre -> right != nullptr && pre -> right != cur)
                pre = pre -> right;
            if(pre -> right == nullptr) // 前驱节点右指针为空说明还没有遍历过cur的左子树
            {
                pre -> right = cur;
                cur = cur -> left;
            }
            else    // 否则说明已经遍历过cur的左子树，将前驱节点右指针重新设置为空
            {
                pre -> right = nullptr;
                res.emplace_back(cur -> val);
                cur = cur -> right;
            }
        } 
    }
    return res;
 }

复杂度分析：

• 其中 \(n\) 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次，因此总时间复杂度为 \(O(2n)=O(n)\)。
• 空间复杂度：\(O(1)\)。

后序遍历

后续遍历思路依然同上，不同的仍然是把cur加入答案的时机，思路如下：

1. 如果cur的左子节点为空，遍历cur的右子节点；
2. 如果cur的左子节点不为空，在cur的左子树中找到cur在中序遍历下的前驱节点：
   • 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为cur。cur更新为cur的左子节点。
   • 如果前驱节点的右子节点不空，也就是前驱节点的右子节点为cur，说明我们已经遍历完 cur 的左子树，将它的右子节点重新设为空。倒序输出从当前节点的左子节点到该前驱节点这条路径上的所有节点。然后将cur更新为cur的右子节点。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

 void addPath(vector<int> &res, TreeNode* root)
 {
    int count = 0;
    while(root != nullptr)
    {
        res.emplace_back(root -> val);
        root = root -> right;
        count++;
    }
    reverse(res.end() - count, res.end());
 }

 vector<int> postorderTraversal(TreeNode *root) 
 {
    vector<int> res;
    if(root == nullptr)
        return res;

    TreeNode* cur = root, * pre = nullptr;
    while(cur != nullptr)
    {
        pre = cur -> left;
        if(pre != nullptr)  // 左孩子不空寻找cur左子树的前驱节点
        {
            while(pre -> right != nullptr && pre -> right != cur)
                pre = pre -> right;
            if(pre -> right == nullptr)     // 为空说明左子树尚未遍历，将pre的右孩子更新为cur
            {
                pre -> right = cur;
                cur = cur -> left;
                continue;
            }
            else        // 否则说明左子树已经遍历，将pre右孩子重新置空
            {
                pre -> right = nullptr;
                addPath(res, cur -> left);
                cur = cur -> right;
            }
        }
        else    // 左孩子为空直接访问右子树
            cur = cur -> right;
    }
    addPath(res, root); // root节点没有parent，所以root需要单独addPath
    return res;
}

Morris的后续遍历其实就是不断把cur节点左孩子到其前驱节点倒序输出的过程，所以由于root节点没有parent，最后要再单独对root节点调用addPath。

复杂度分析：

• 时间复杂度：\(O(n)\)，其中 \(n\) 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
• 空间复杂度：\(O(1)\)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

上面这种解法是leetcode的官方解法，这里我还有另外一种思路，如上面所说，Morris的后续遍历其实就是不断把cur节点左孩子到其前驱节点倒序输出的过程，那么是否可以采用Morris的方法将输出顺序改为cur、cur的右孩子、cur的左孩子，在输出完之后再统一对res进行翻转？

代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

vector<int> postorderTraversal(TreeNode *root) 
{
    vector<int> res;
    if(root == nullptr)
        return res;
    TreeNode* cur = root, * pre = nullptr;
    while(cur != nullptr) 
    {
        
        pre = cur -> right;
        if(pre == nullptr)  // cur右孩子为空，直接将cur加入答案并访问左子树
        {
            res.emplace_back(cur -> val);
            cur = cur -> left;
        }
        else    // 否则寻找 `父右左` 遍历模式下的前驱节点
        {
            while(pre -> left != nullptr && pre -> left != cur)
                pre = pre -> left;
            if(pre -> left == nullptr)  // 为空说明右子树尚未遍历
            {
                res.emplace_back(cur -> val);
                pre -> left = cur;
                cur = cur -> right;
                continue;
            }       
            else    // 否则说明右子树已经遍历
            {
                pre -> left = nullptr;
                cur = cur -> left;
            }
        }
    }
    reverse(res.begin(), res.end());    // 翻转数组
    return res;
}

复杂度分析：

• 时间复杂度：\(O(n)\)，其中 \(n\) 是二叉树的节点数。没有右子树的节点只被访问一次，有右子树的节点被访问两次，最后翻转数组。
• 空间复杂度：\(O(1)\)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

二叉树问题的小trick

二叉树中有一类问题其实套路是固定的，虽然不同问题要求的东西不一样，但是仔细分析会发现，其实它们用到的套路是一样的。当一个问题的结果需要树的左右子树也满足条件，且每层子树需要返回的参数一样时，便可以用到递归套路。

一棵子树上的点在深度优先搜索序列（即先序遍历）中是连续的

可以采用这个套路来求解一个树是否是另一个树的子树，但是但从一个树s的dfs遍历是否是另一个树t的dfs遍历的字串并不能判断出是否是子树，所以想要通过dfs的序列判断s是否是t的子树，还需要做一些额外的处理。

可以通过引入两个空值 lNull 和 rNull，当一个节点的左孩子或者右孩子为空的时候，就插入这两个空值，这样深度优先搜索序列就唯一对应一棵树。处理完之后，就可以通过判断「s的深度优先搜索序列包含 t 的深度优先搜索序列」来判断s是否是t的子树。

这里判断s的遍历序列是否是t遍历序列的子串可以用KMP算法或Rabin-Karp算法

后序遍历迭代法

采用迭代法的后序遍历，即上边用栈的方法，当遍历到节点 \(p\) 时，栈中的节点刚好是 \(p\) 的祖先节点，所以此时将栈中节点依次弹出便得到 \(p\) 的祖先节点的倒序。

验证二叉搜索树

问题：给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

分析：如何判断一个二叉树是否是二叉搜索树？它需要满足两个条件：

1. 它的左子树和右子树都是二叉搜索树；
2. 它的节点值大于左子树的最大值且小于右子树的最小值。

那么从以上两点出发，就可以构造一个递归套路，每层需要向上层返回自己这颗树是否是二叉搜索树，如果不是那么整个树一定不是二叉搜索树；同时还要向上层返回自己这颗子树的最大值和最小值。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

bool isValidBST(TreeNode* root) 
{
    return isBST(root, LONG_MIN, LONG_MAX);
}

bool isBST(TreeNode * root, long lower, long upper)
{
    if(root == nullptr) // base case
        return true;
    if(root -> val >= upper || root -> val <= lower)
        return false;
    return isBST(root -> left, lower, root -> val) && isBST(root -> right, root -> val, upper);
}

这里是反向思维，若cur的值需要大于左子树最大值并且小于右子树最小值，那么就等价于让它的左子树判断其最大值是否小于cur值以及cur右子树判断其最小值是否大于cur值.

验证平衡二叉树

问题:给定一个二叉树，判断它是否是高度平衡的二叉树。

分析:一个二叉树是平衡二叉树,那么它必然满足它的左右子树都是平衡二叉树,且左右子树的高度差的绝对值不大于1.那么就又可以以相似的方式构造递归,每次需要向上层返回的参数有:

• 当前子树是否是平衡二叉树
• 当前子树的深度

代码:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
bool isBalanced(TreeNode* root) 
{
    int height;
    bool is_balance;
    isBalancedTree(root, is_balance, height);
    return is_balance;
}

void isBalancedTree(TreeNode* root, bool &is_balance, int &height)
{
    if(root == nullptr)
    {
        is_balance = true;
        height = 0;
        return ;
    }
    bool left_balance, right_balance;
    int left_height, right_height;
    isBalancedTree(root -> left, left_balance, left_height);
    isBalancedTree(root -> right, right_balance, right_height);
    if(!left_balance || !right_balance || abs(left_height - right_height) > 1)
        is_balance = false;
    else
        is_balance = true;
    height = max(left_height, right_height) + 1;
}

完全二叉树的第k个节点

规定根节点位于第 \(0\) 层，完全二叉树的最大层数为 \(h\)。根据完全二叉树的特性可知，完全二叉树的最左边的节点一定位于最底层，因此从根节点出发，每次访问左子节点，直到遇到叶子节点，该叶子节点即为完全二叉树的最左边的节点，经过的路径长度即为最大层数 \(h\)。

当 \(0 \le i < h\) 时，第 \(i\) 层包含 \(2^i\) 个节点，最底层包含的节点数最少为 \(1\)，最多为 \(2^h\)。

因此对于最大层数为 hhh 的完全二叉树，节点个数一定在 \([2^h,2^{h+1}-1]\) 的范围内，可以在该范围内通过二分查找的方式得到完全二叉树的节点个数。

如何判断第 \(k\) 个节点是否存在呢？如果第 \(k\) 个节点位于第 \(h\) 层，则 \(k\) 的二进制表示包含 \(h+1\) 位，其中最高位是 \(1\)，其余各位从高到低表示从根节点到第 \(k\) 个节点的路径，\(0\) 表示移动到左子节点，\(1\) 表示移动到右子节点。通过位运算得到第 \(k\) 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 \(k\) 个节点是否存在。

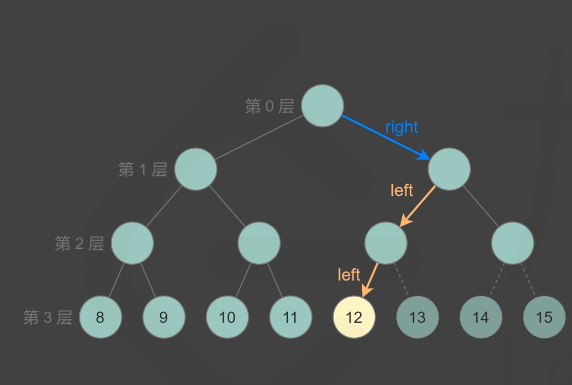
那么如何依次判断k的各个二进制位是否为1呢？这里需要一个\(bits = 2^{h-1}\)，\(h\)为要查找节点所在层数(注意根节点是0层),比如现在要查找\(8\)这个节点，那么\(bits = 2^{3 - 1} = 0100\),而\(8\)的二进制表示是\(1000\),用\(bits\) & \(1000 = 0\)，所以向左子树走，然后将\(bits\)左移一位，再与\(8\)（也就是\(1000\)）相与得到\(0010 \& 1000 = 0\),继续向左子树移动，重复上面操作，一直到\(bits\)为\(0\)为止，此时节点若不为空，那么就是第\(8\)个节点。