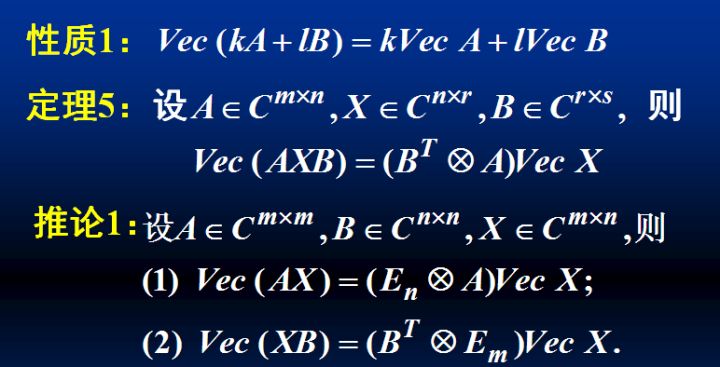线性空间

线性空间

线性空间定义：

线性子空间定义：

平凡子空间：\(V\)空间的平凡子空间指\(0\)空间和\(V\)空间本身，其他维数的空间都是非平凡子空间。

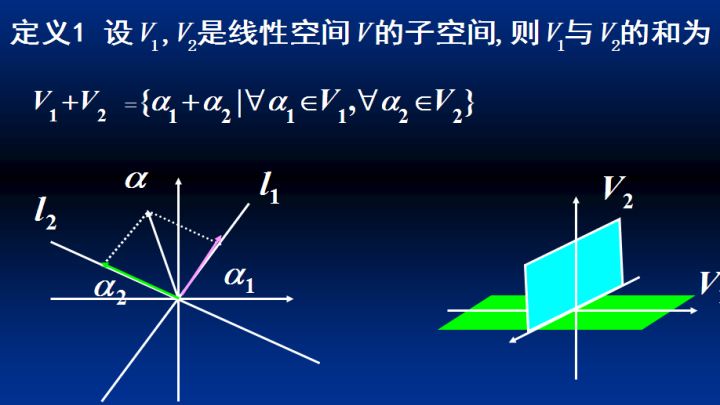
线性空间的和：

维数定理

直和

判断线性空间V的两个子空间\(V_1\)和\(V_2\)是否是直和的方法

判断\(V_1 \cap V_2 = \{0\}\)是否成立，若成立，就是直和；否则不是直和。

将子空间的概念推广到多个子空间，于是在多个子空间中就可以定义这样的直和关系：

酉空间

欧几里得空间：定义了内积的实线性空间。

欧几里得空间的定义推广到复线性空间就是酉空间。

正交补子空间

这里的\(V_n(C)\)指的是酉空间。这里的\(n\)表示维数，\(C\)表示复数空间。这个定义指的是复数域内的\(n\)维空间，即是酉空间。

也就是说，一个空间V的子空间\(V_1\)和\(V_2\)不仅要满足直和的关系，还要相互正交。这样的空间我们称\(V_2\)为\(V_1\)的正交补子空间（或简称正交补）。显然，二者是互为正交补的。正交补分解实际上就是在分正交基。直和分解实际上就是在分解基向量。

定理：\(V_n(C)\)的任意子空间\(V_1\)都有唯一的正交补。

Kronecker积

Kronecker积

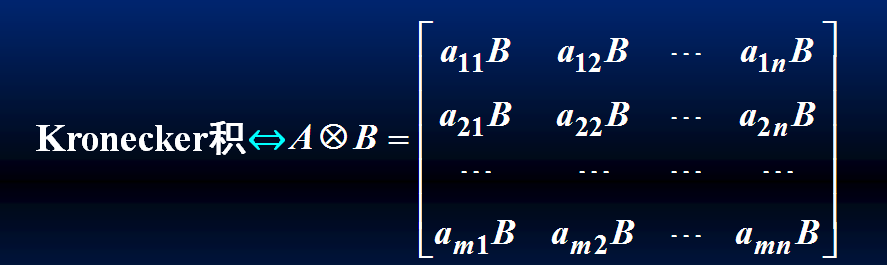
其中\(a_{ij}\)为矩阵\(A\)的第\(i\)行第\(j\)列的元素，对于\(A \in \mathbb{R^{m × n}}\) 和 \(B \in \mathbb{R^{p × q}}\),\(A \otimes B \in \mathbb{R^{(mp) × (nq)}}\)。

Kronecker积的性质如下：

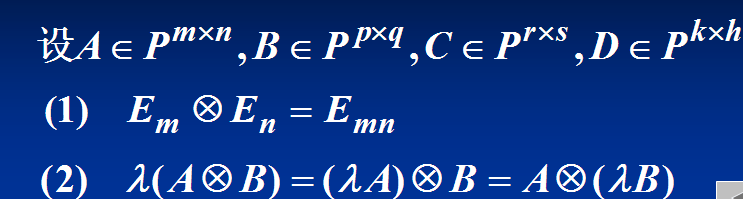
这些性质中前4条与矩阵运算完全相同，从第5条开始是Kronecker积独有的性质。

给出一些定义和定理：

Kronecker积的特征值：

Kronecker和

由定义2我们可以看到，对于Kronecker积而言，m阶矩阵和n阶矩阵之间是无法直接求和的，所以，我们通过对单位阵的Kronecker积运算，同时把他们化为\((m × n)\)阶方阵，这样就可以对矩阵进行求和运算了。

向量化算符

性质：