常见的随机过程
正态过程
多维正态分布的概率密度和特征函数

记 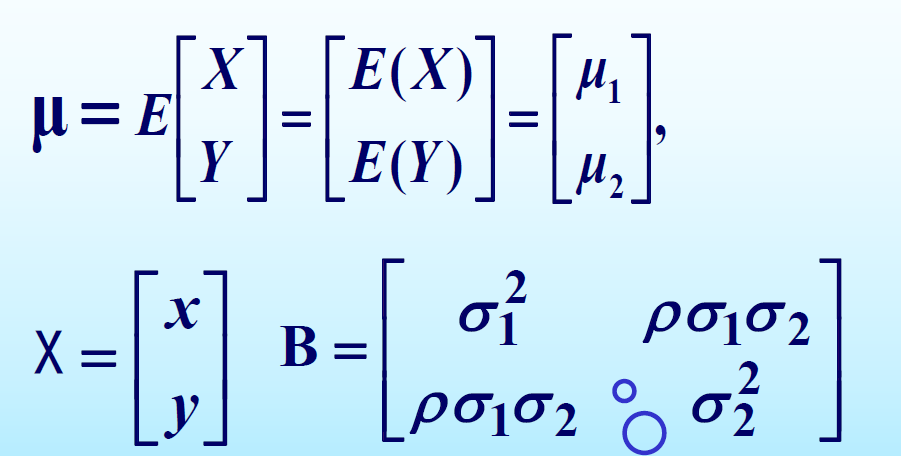
则\((X,Y)\)的联合概率密度为
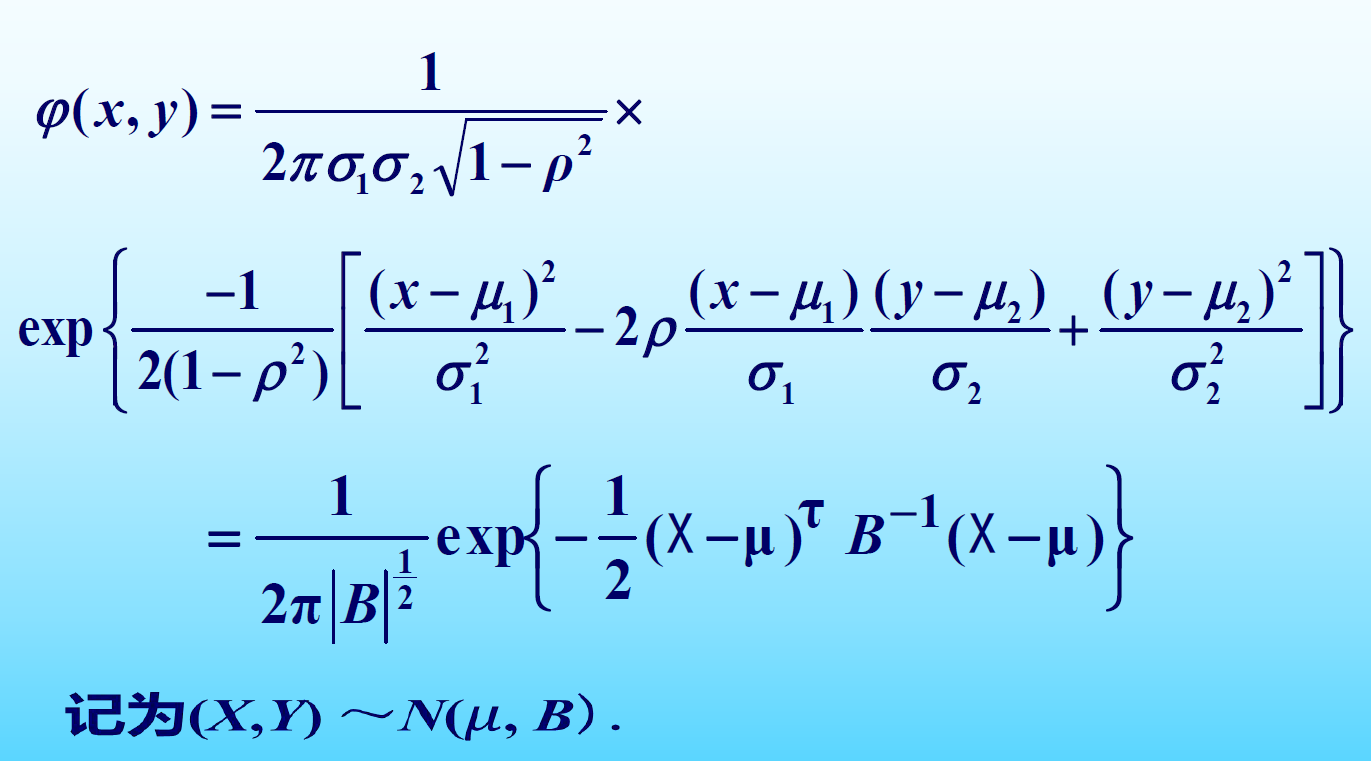

证明随机过程\(X(t)\)是正态过程
要证明随机过程\(X(t)\)是正态过程,即证对\(\forall t_1,t_2,\dots\) , \(t_n,(X(t_1),X(t_2),\dots,X(t_n))\)是\(n\)维正态分布。
方法1:用特征函数
方法2:正态分布的线性不变性
正态分布的线性不变性:

正态分布的线性变换不变性:

维纳过程


维纳过程的分布

设\(t>s\),因\(W(0)=0\),且\(W(t)\)是平稳独立增量过程,故
\[W(t) - W(s) = W(t-s+s)- W(s)\]
与
\[W(t-s) - W(0) = W(t-s)\] 有相同分布\(N(0,\sigma^2 (t-s))\)。
维纳过程是正态过程。
维纳过程的数字特征
维纳过程是平稳独立增量过程,其数字特征如下。
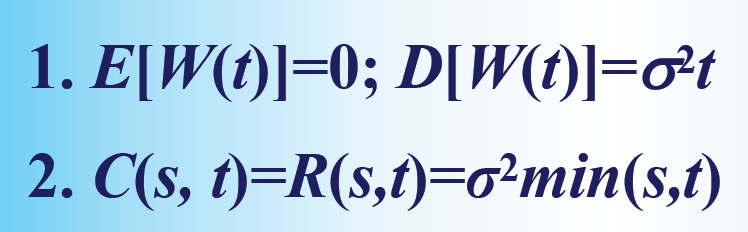
计数过程和泊松过程
定义
计数过程:


Poisson过程是一类很重要的计数过程。
Poisson过程数学模型:


齐次泊松过程

泊松过程的等价定义


齐次泊松过程的有关结论
数字特征
均值函数: \(m(t)=E\{N(t)\}=\lambda t\)
方差函数: \(D(t)=\lambda t\)
协方差函数: \(C(s,t)=\lambda min(s,t)\)
相关函数: \(R(s,t)=\lambda min(s,t)+\lambda^2 st\)
故有\(\lambda=\frac{E\{N(t)\}}{t}\),称\(\lambda\)为事件的到达率或单位时间内事件出现的平均次数。
时间间隔与等待时间的分布
如下图所示,\(N(t)\)是轨道是跃度为\(1\)的阶梯函数。
的分布函数.png)
用\(T_n\)表示事件\(A\)第\(n-1\)次出现与第\(n\)次出现的时间间隔。\(W_n\)为事件\(A\)第\(n\)次出现的等待时间(到达时间),则有:
\[W_n=\sum\limits_{i=1}^nT_i\]
和
\[T_n=W_n - W_{n-1}\]

到达时间的条件分布


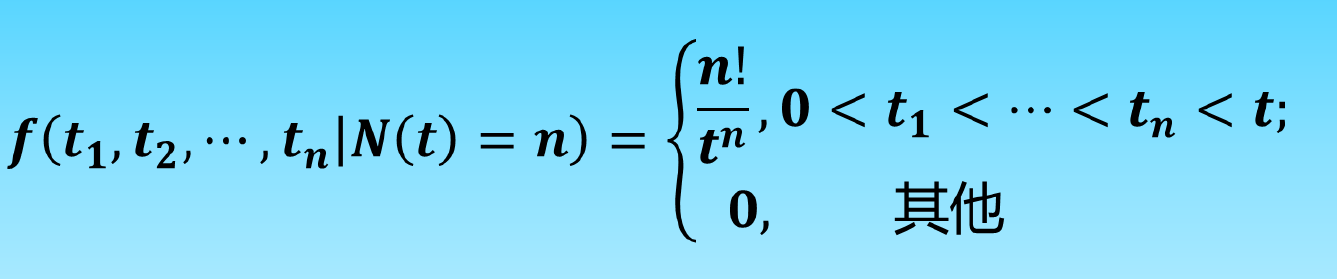


常见的随机过程
https://gstarmin.github.io/2023/02/18/常见的随机过程/