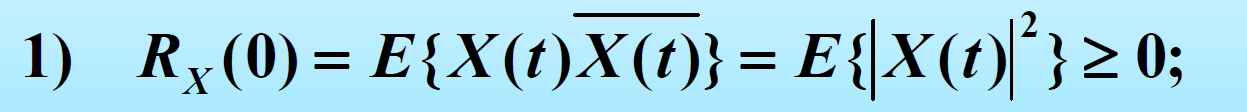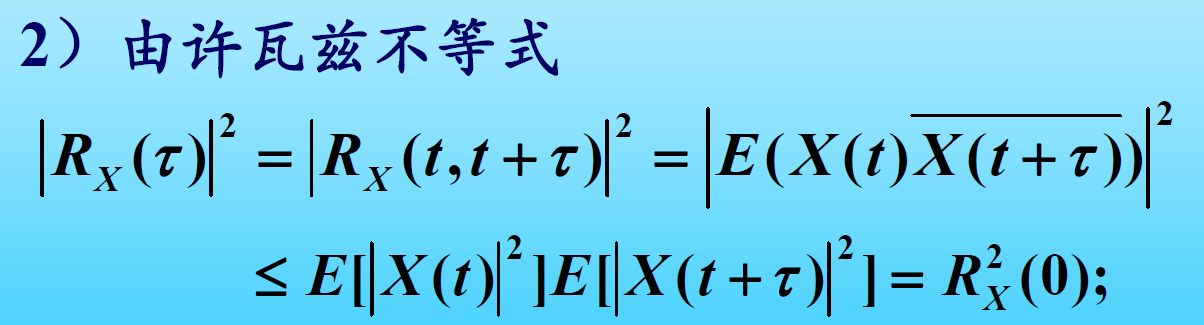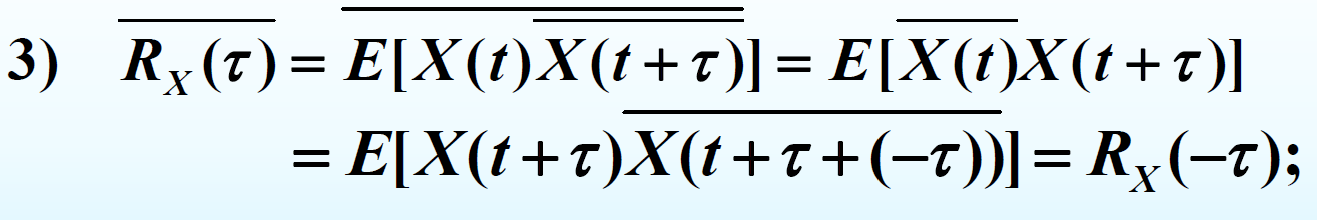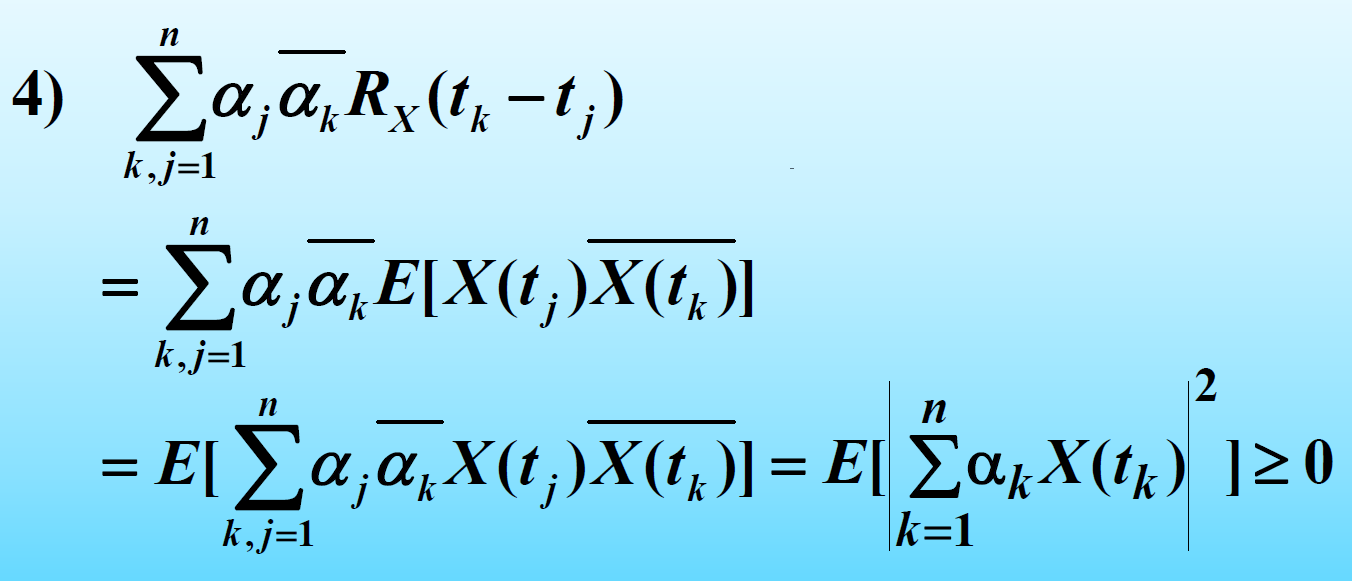平稳过程

严平稳过程

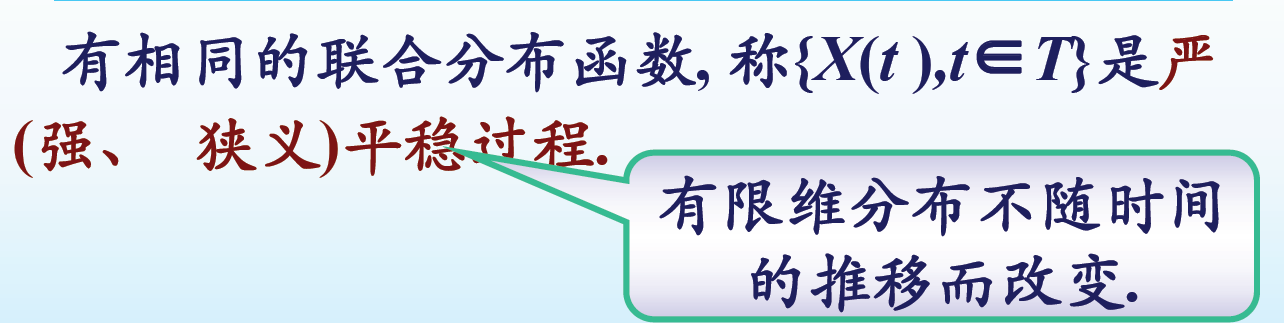
严平稳过程有限维分布不随时间的推移而改变，，它的当前变化情况与过去的情况有不可忽视的联系。

严平稳过程的一维分布与时间无关，而二维分布仅与\(t_1\)和\(t_2\)的时间间隔有关，与时间起点无关。

宽平稳过程

由于

• 工程中确定一个过程的有限维分布函数族,进而判定过程的严平稳性十分困难；
• 部分随机过程(如正态过程)的概率特征主要由一阶和二阶矩函数确定；
• 工程实际中,通常仅需在相关理论范畴内考虑平稳过程,即只限于研究一、二阶矩（均值、相关函数等）理论.

所以有了宽平稳过程。

定义：

其中\(R_x(\tau)\)为\(\{X(t),t \in T\}\)的自相关函数。其协方差函数为 \[C_X(s,t)=R_X(s,t)-|m_X|^2=R_X(\tau)-|m_X|^2\]

自协方差函数与自相关函数都仅依赖于\(t－s\)

维纳过程不是宽平稳过程，但是维纳过程是增量宽平稳过程，即 \[X(t)=W(t+a)-W(t), t \ge 0, \quad (a>0)\]

是宽平稳过程

两种平稳性的关系

• 严平稳过程不一定是宽平稳的;

因宽平稳过程一定是二阶矩过程, 而严平稳过程未必是二阶矩过程.

• 宽平稳不一定 严平稳;
• 严平稳过程是宽平稳过程的充要条件是其二阶矩存在.
• 对于正态过程, 宽平稳性与严平稳性等价.

平稳过程的自相关函数

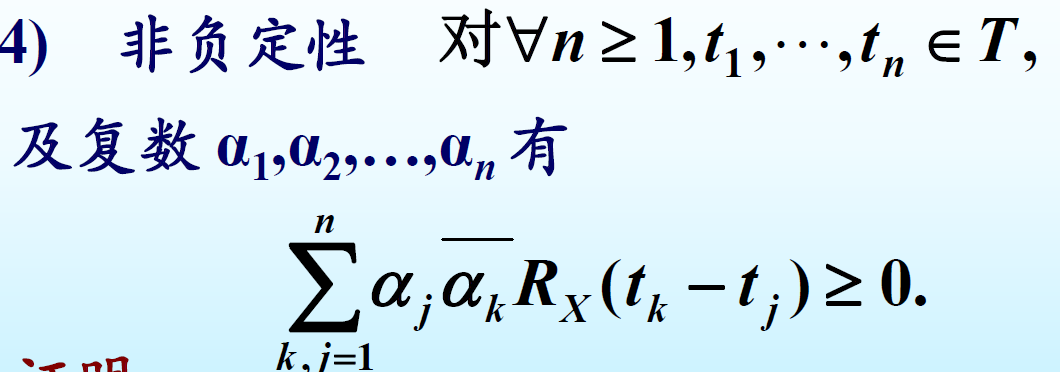
证明:

1. 
2. 
3. 
4. 

推论：

定理：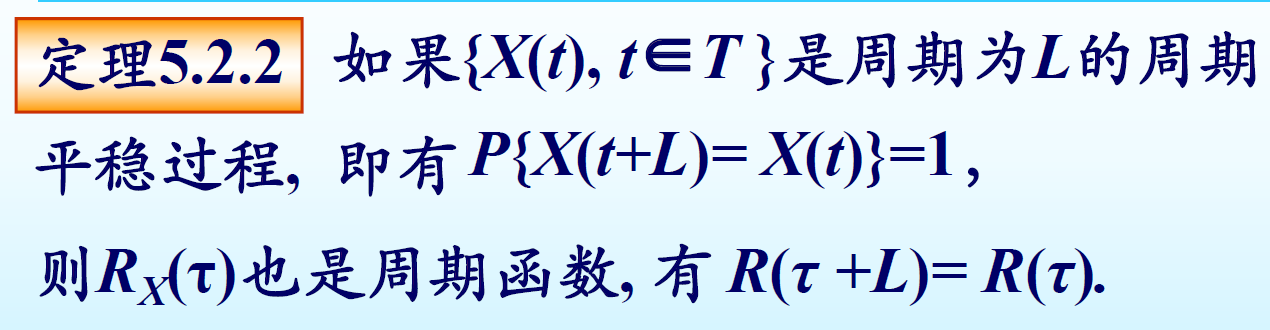

证明：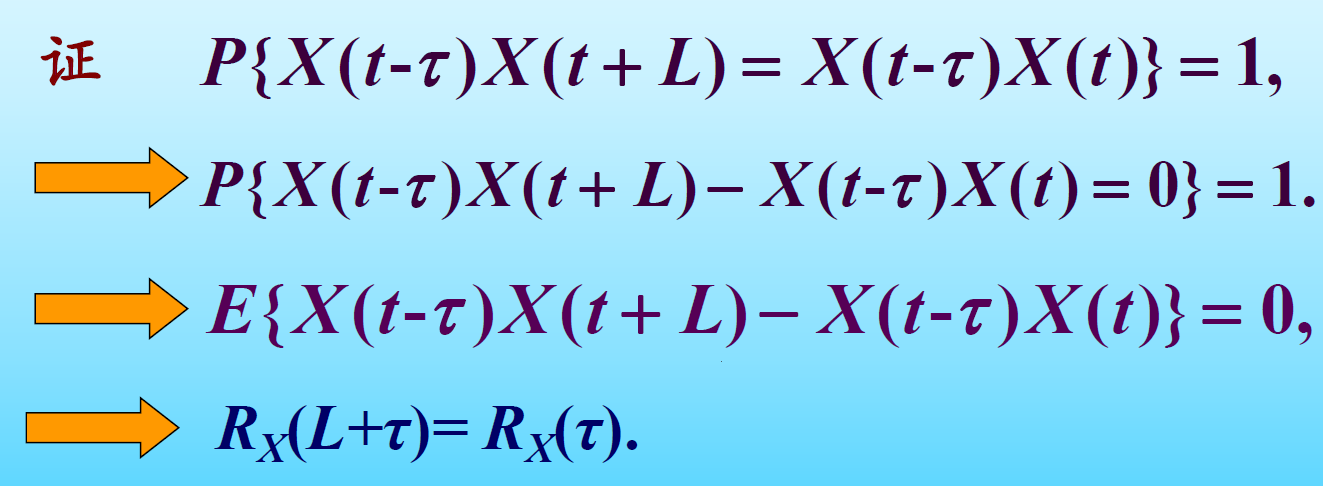

定理:

定理：

推论：