广义逆矩阵

单边逆

所谓矩阵的单边逆就是指矩阵的左逆和右逆。

矩阵的单边逆

定理1:设 \(A \in \mathbb{C}^{m × n}\),则

• \(A\)左可逆的充要条件是\(A\)为列满秩矩阵
• \(A\)右可逆的充要条件是\(A\)为行满秩矩阵

推论1:设 \(A \in \mathbb{C}^{m × n}\),则

• \(A\)左可逆的充要条件是\(N(A)=\{0\}\)
• \(A\)右可逆的充要条件是\(R(A)=\mathbb{C}^m\)

单边逆的求法

例1:

例2:

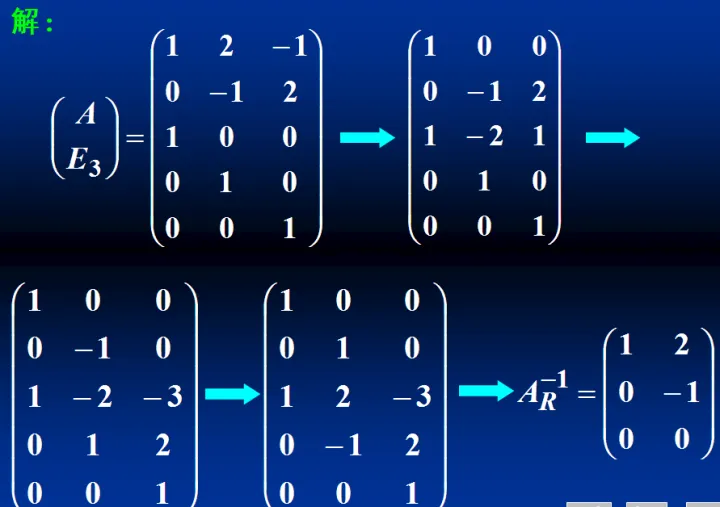
需要注意的是例1求左逆矩阵进行的是初等行变换,例2求右逆矩阵是进行的初等列变换，初等行变换我们在线性代数中常用，比较熟悉，但是要求右逆矩阵一定要进行初等列变换。

广义逆矩阵

定义:

性质: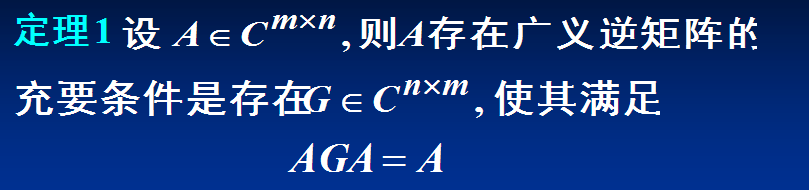

推论: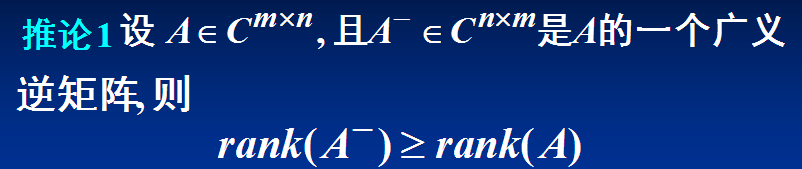

需要注意的是，同线性代数中的矩阵的逆不同的是，这里求的广义逆一般不唯一。既然不唯一，有许多解的话，我们就考虑是否有一个通解可以将所有的广义逆全部表示呢？的确有，下面我们就介绍定理2，该定理表示的就是全部的广义逆：

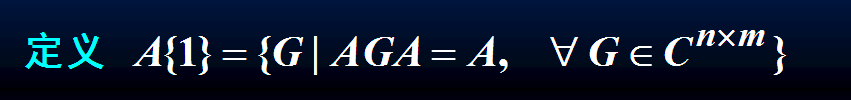
定理2(不常考):

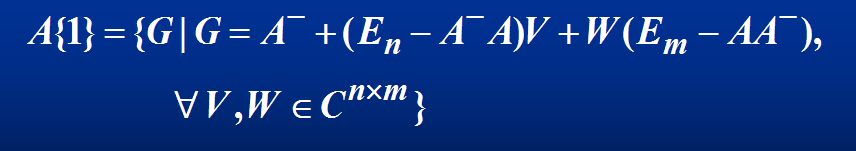
定理3:

• (i)是逆矩阵性质在广义逆的推广
• (ii)说的是一个矩阵乘以他的广义矩阵是幂等矩阵，且他们矩阵的秩相等
• (iii)可以看出0矩阵的广义逆矩阵可以是任何矩阵（包括0矩阵）
• (v)说的是\(AA^{-1}\)与\(A\)的值域相同,\(A^{-1}A\)与\(A\)的零空间相同,证明如下:

自反广义逆矩阵

自反广义逆矩阵是广义逆矩阵里的一类特殊矩阵,其定义如下: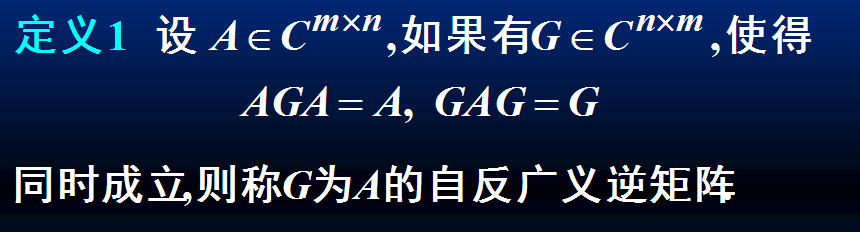

定理1:

需要注意的是，自反广义逆矩阵并不唯一。事实上，对于

构造这样的矩阵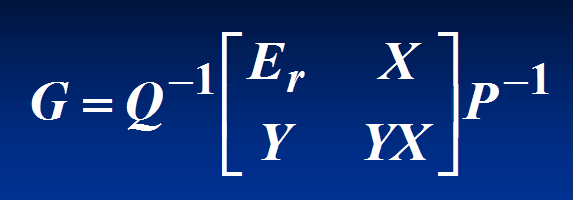

所有满足这样条件的矩阵G，就是A的自反广义逆。所以自反广义逆并不唯一.

定理2(考试不要求):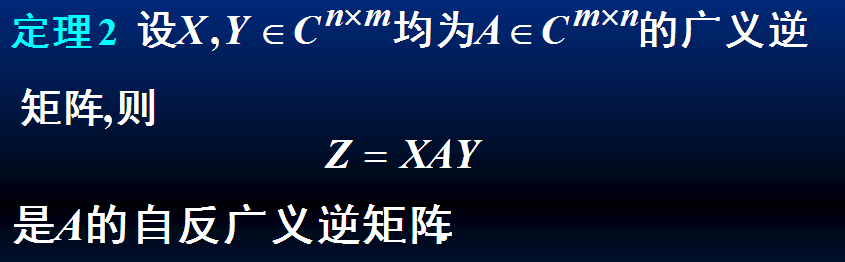

定理2给出了自反广义逆矩阵的一种具体的构造方法,

定理3:

定理3给出了在广义逆矩阵中，区分自反广义逆的一种有效方法。当广义逆矩阵的秩等于矩阵A的秩的时候是自反广义逆。当广义逆的秩大于矩阵A的秩的时候是广义逆矩阵而不是自反广义逆矩阵。

M-P广义逆矩阵

M-P广义逆矩阵（Moore-Penrose）矩阵是在自反广义逆矩阵之上又加了两个条件形成的矩阵，要求更加苛刻。我们一般用 \(A^+\) 来表示M-P广义逆矩阵。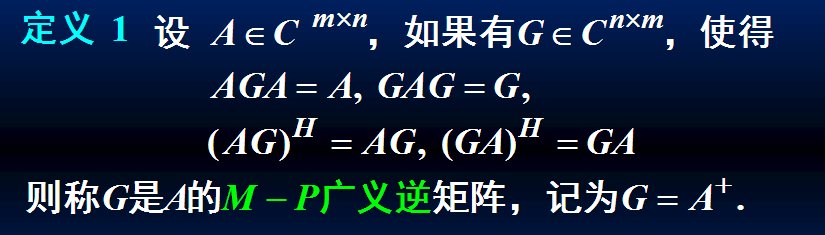

这四个条件，共同保证了 \(A^+\) 的唯一性。

定理1:

该定理给出了\(A^+\) 的具体计算方法。定理的证明直接用该式子验证定义中的四个式子即可.

定理2:设 \(A \in \mathbb{C}^{m × n}\),则 \(A^+\)是唯一的.

这一点已经在上面提到过了,定义中的四个式子保证了\(A^+\)的唯一.

M-P广义逆的性质

定理5: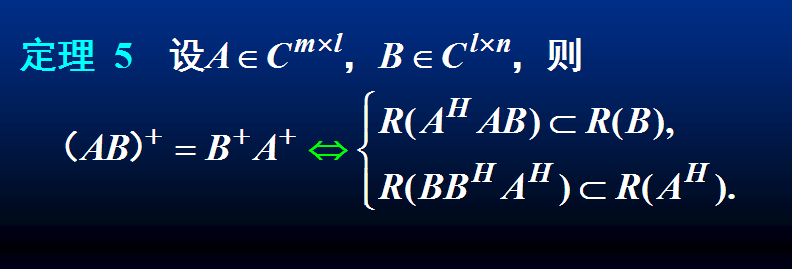

M-P广义逆的计算

最大秩分解

定理1: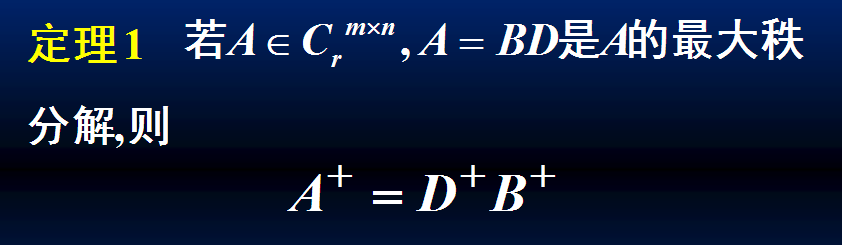

例1:

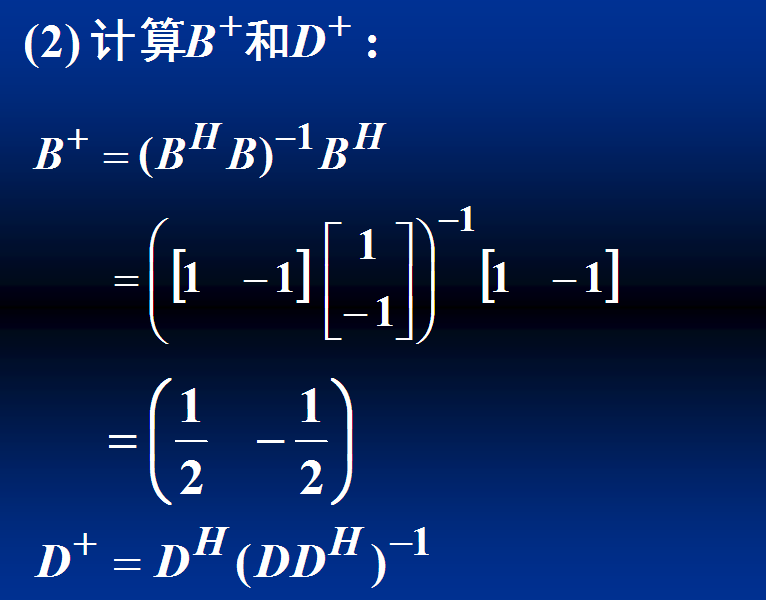
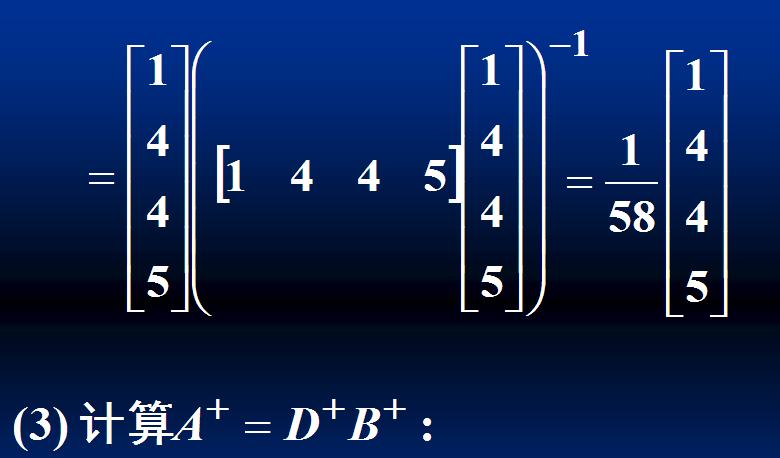
奇异值分解法

定理2:

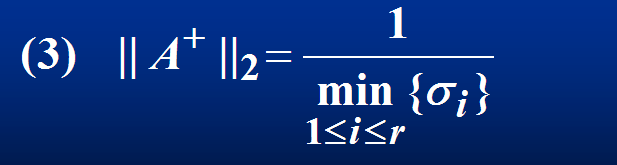
M-P广义逆的应用

判断方程有没有解

求出\(A^+\),判断\(AA^+b\)是否等于\(b\),若不等于则没有解，否则有解。

求方程的最佳逼近解/最小范数解/最小二乘解

当方程有解的时候，可以求得最小范数解为\(A^+b\)；当方程没有解的时候，可以求出最佳逼近解为\(A^+b\)，最小二乘通解为\(A^+ b+(I-A^+ A)u, \forall u \in \mathbb{C}^n\),其中\(A\)为\(n\)阶矩阵。