矩阵函数

矩阵函数

定义： 设幂级数\(\sum\limits_{k=0}^{\infty} c_k z^k\)收敛半径为\(r\)，且当\(|z|<r\)的时候，幂级数收敛于\(f(z)\)，即

\[f(z)=\sum\limits_{k=0}^{\infty} c_kz^k, |z|<r\]

如果\(A \in \mathbb{C}^{n×n}\)满足\(r(A)<r\),则收敛的矩阵幂级数\(\sum\limits_{k=0}^{\infty} a_kA^k\)的和为矩阵函数，记为\(f(A)\)，即

\[f(A)=\sum\limits_{k=0}^{\infty} c_k A^k\]

把\(f(A)\)的方阵换为\(At\),\(t\)为参数，得到

\[f(At)= \sum\limits_{k=0}^{\infty}c_k(At)^k\]

常见的矩阵级数有：

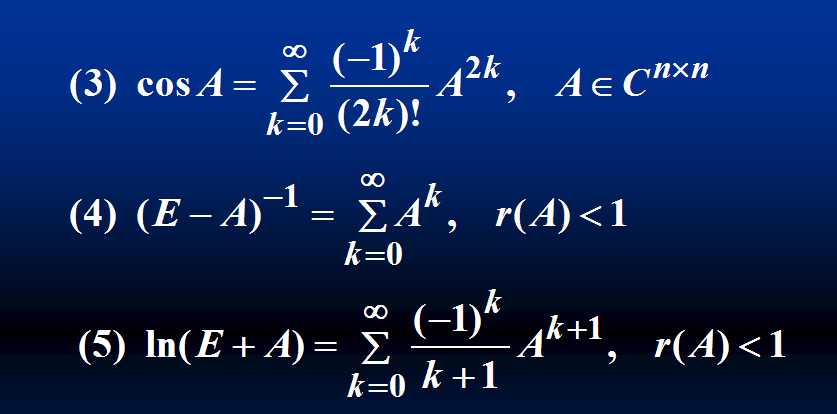
矩阵函数的计算方法

利用相似对角化

设\(P^{-1}AP= diag(\lambda_1,\lambda_2, \dots, \lambda_3) = D\)

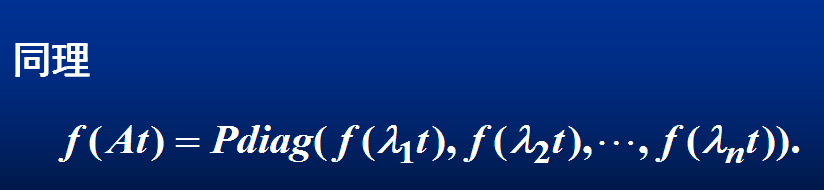
例1：

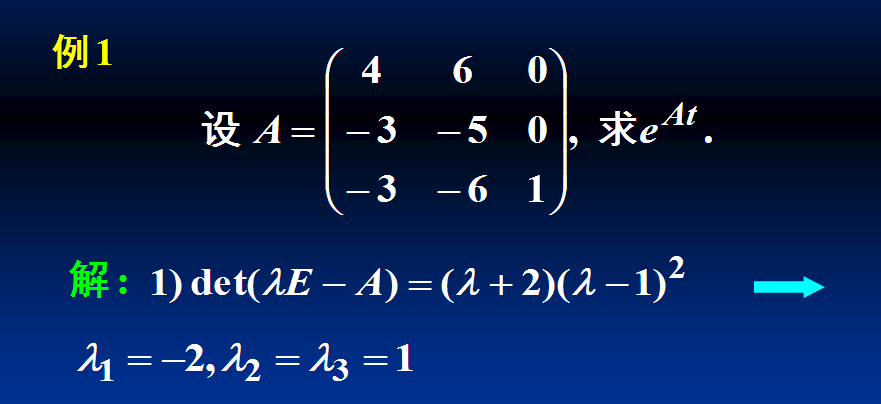
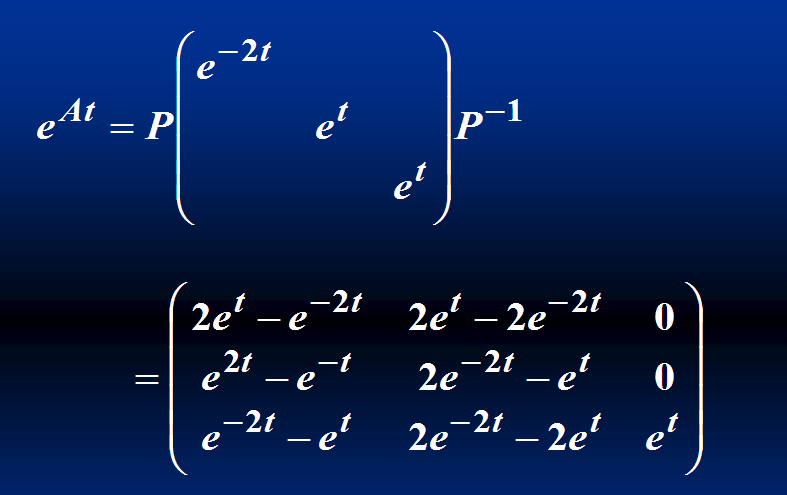
Jordan标准型法

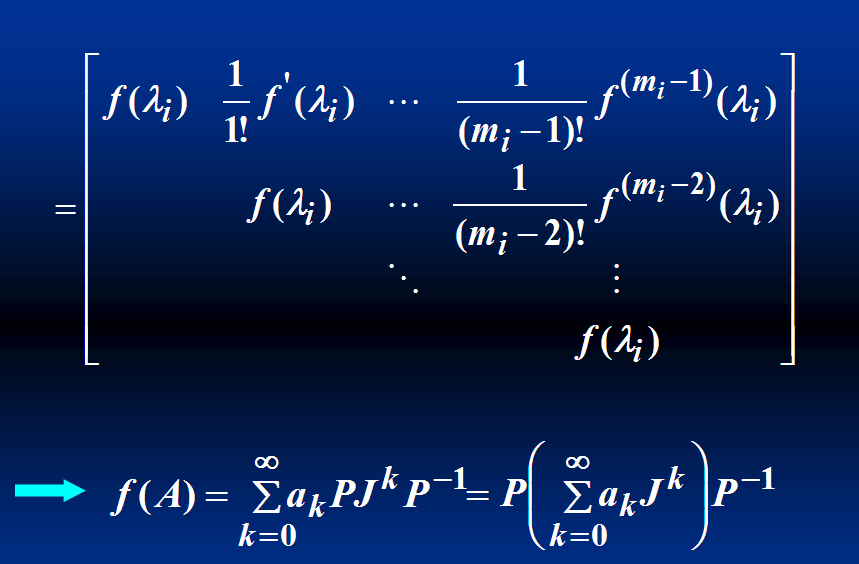
例2：

数项级数求和法

由哈密尔顿-凯莱定理于是我们有：

由该定理，我们可以实现降次的目的。

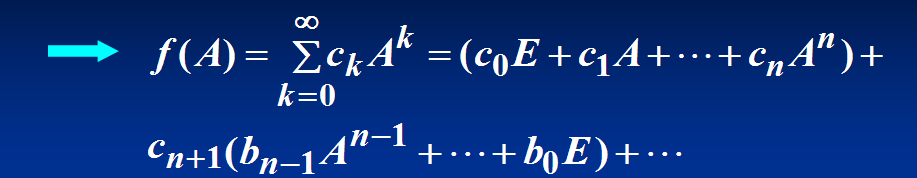
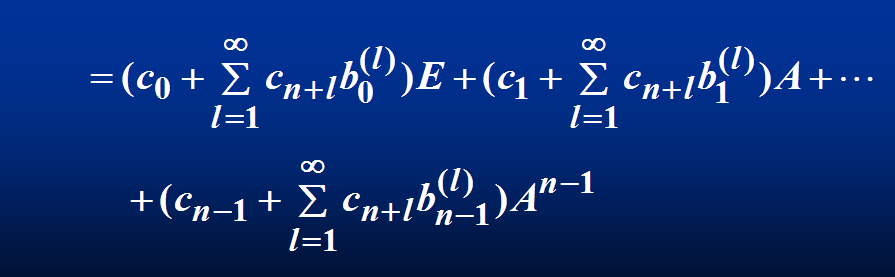
矩阵函数的性质