特征值估计
shur不等式 
证明如下: 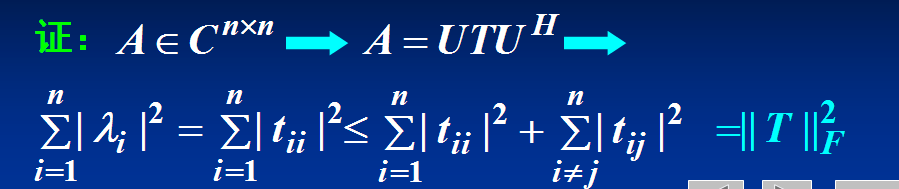
行盖尔圆盘和列盖尔圆盘: 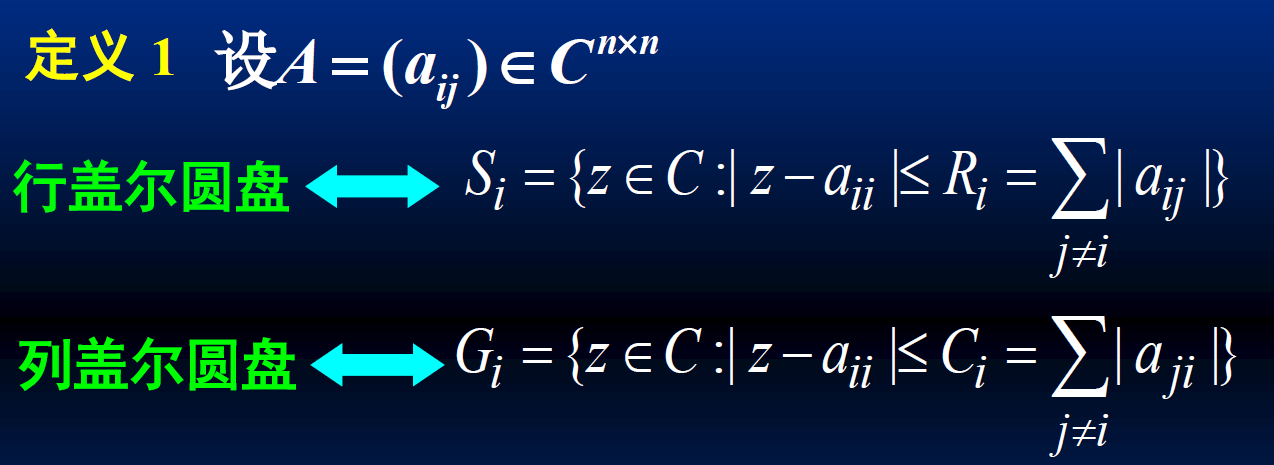
圆盘定理: 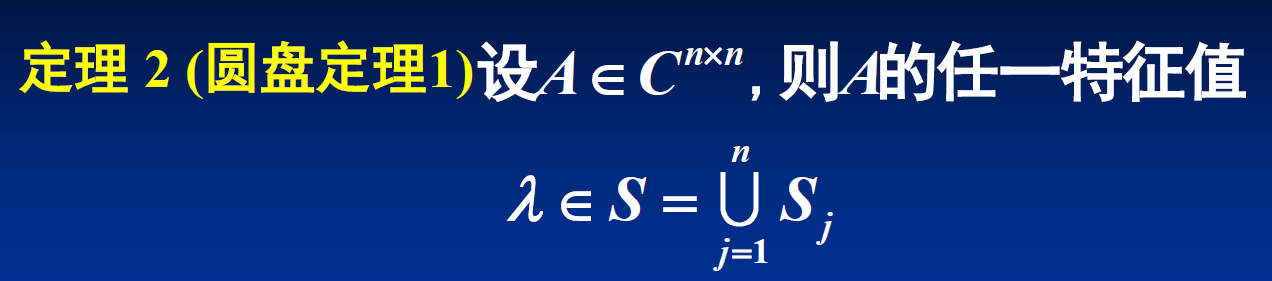

推论1:设\(n\)阶方阵\(A\)的\(n\)个盖尔圆盘两两互不相交,则\(A\)相似于对角阵.
推论2: 设\(n\)阶实阵\(A\)的\(n\)个盖尔圆盘两两互不相交,则\(A\)特征值全为实数.
对角占优矩阵:

Rayleigh商:设\(A \in \mathbb{C}^{n \times n}\)为Hermite矩阵,\(x \in \mathbb{C}\),称 \[R(x)=\frac{x^HAx}{x^Hx}, x \ne 0\]
为\(A\)的Rayleigh商。
定理(Rayleigh-Ritz): 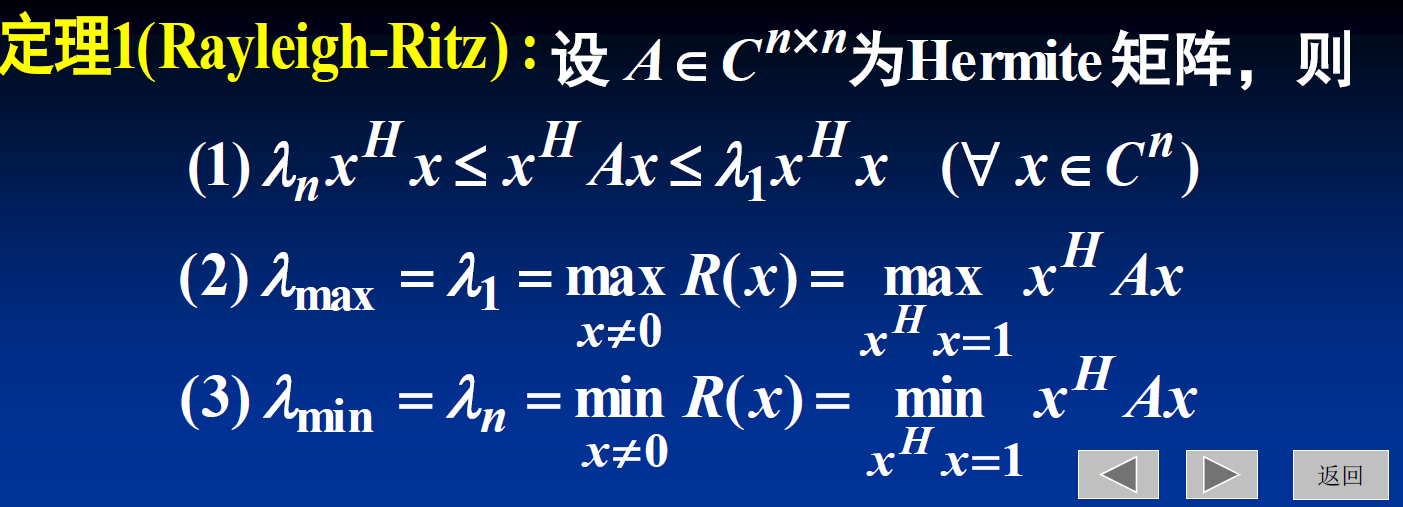
特征值估计
https://gstarmin.github.io/2022/12/04/特征值估计/