近似算法
近似算法
假设现在需要解决一个NP-Hard问题,但是又不太可能在多项式时间内求解,但是我们可以退而求其次,那么就必须要牺牲下面的其中一项:
- 求得最优解
- 在多项式时间内完成
- 覆盖问题的所有例子
而牺牲第二条是不能接受的,当我们选择满足后两者(也就是牺牲第一项),即对解的优越性放宽要求时,设计出的算法被称为近似算法。
Load Balancing问题
给定\(m\)台相同的机器,\(n\)个任务,任务\(j\)需要的处理时间为\(t_j\),且每个任务\(j\)必须在一台机器上连续完成。
令\(J(i)\)为分配给机器\(i\)的任务子集,机器\(i\)的负载为\(L_i=\sum\limits_{j \in J(i)}t_j\),该问题的时间跨度(makespan)为所有机器上的结束时间最大值\(L=\max\limits_i L_i\)。
Load Balancing:求上述问题中的任务分配使得时间跨度最小。
贪心算法
每次将任务\(j\)分配在当前负载最小的机器上: 
引理1:最优解makespan\(L^* \ge \max\limits_j t_j\)。
用时最长的这个任务总需要分配到一个机器上完成.
引理2:最优解makespan \(L^* \ge \frac{1}{m} \sum\limits_j t_j\)
所有任务的总运行时间为\(\sum\limits_j t_j\),那么\(L^*\)的时间跨度必然选自\(m\)个机器中最大的一个,而\(m\)个机器中的最大时间跨度一定不小于\(\frac{1}{m}\)的总运行时间.
定理:贪心算法是Load Balancing问题的二倍近似算法。
证明:
假设负载\(L_i\)为问题的平静,令\(j\)为最后一个分配到该机器的任务,由贪心算法,在任务\(j\)分配之前,机器\(i\)的负载是最小的.\(j\)分配之前机器\(i\)的负载为\(L_i - t_j\),也就是说在准备分配\(j\)的时候有\(L_i - t_j\)小于或等于所有机器上的负载\(L_k, 1 \le k \le m\)

分配任务\(j\)之前,由引理1: \[ \begin{aligned} L_i - t_j &\le \frac{1}{m}\sum\limits_k L_k \\ &= \frac{1}{m} \sum\limits_k t_k \\ &\le L^* \end{aligned}\]
分配任务\(j\)后,由上式以及引理2: \[L_i = (L_i -t_i) + t_j \le L^* + \max\limits_j t_j \le L^* + L^* = 2L^*\]
那么贪心算法是Load Balancing的紧2倍近似算法吗?判断\(\rho\)-近似算法是否紧的要看该算法相比于最优解有比\(\rho\)更低的近似率吗?若有则说明其并不是紧的。
答:大致是的,考虑下面的一个Load Balancing的实例,有\(m\)个机器,\(m^2\)个任务,其中有\(m(m-1)\)个任务运行时间为1,一个任务的运行时间为\(m\).贪心算法的结果如下图所示:
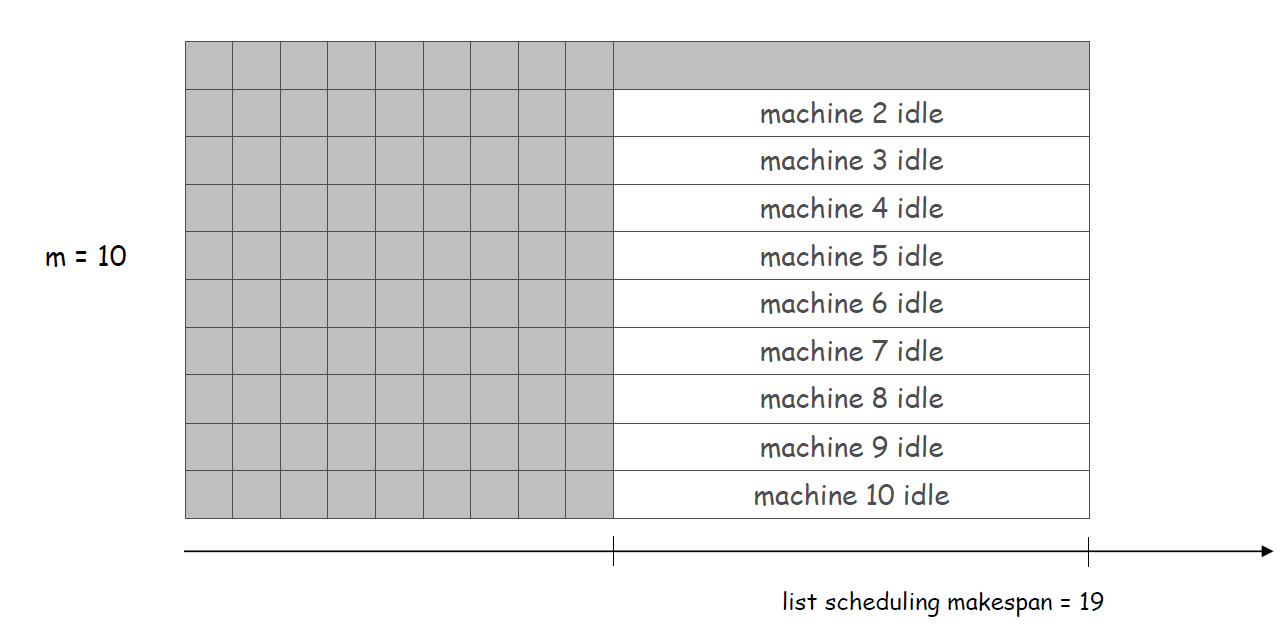
而最优解的结果为:
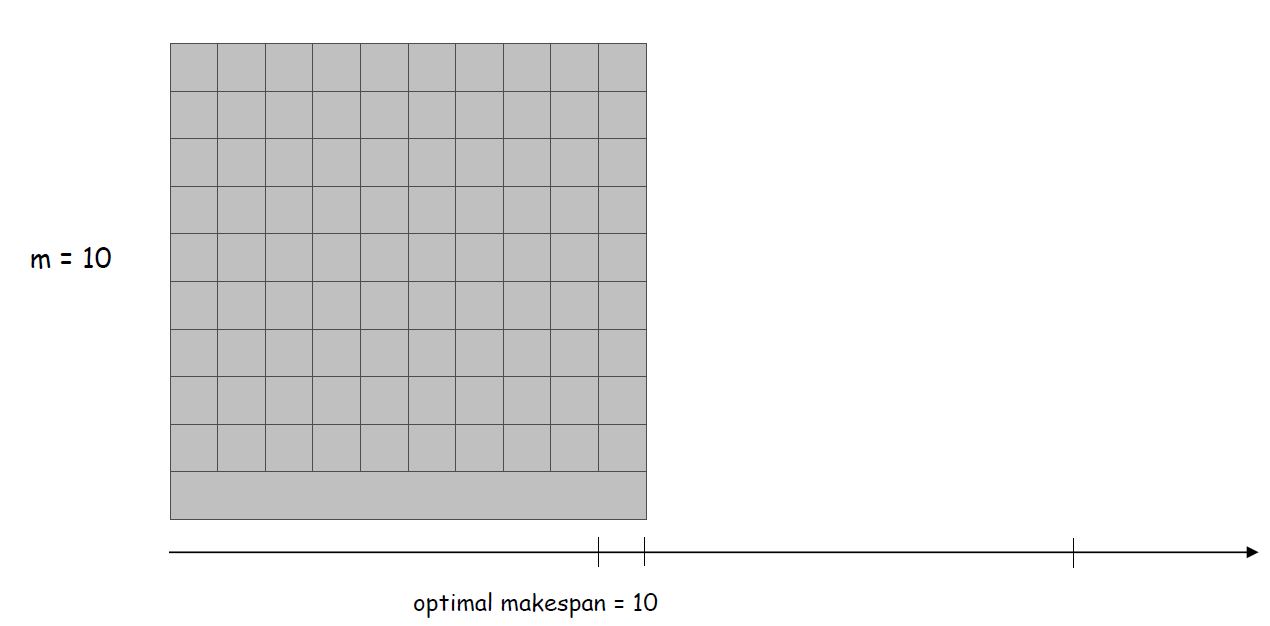
这个实例里贪心算法的时间跨度为19,而最优解的时间跨度为10.
LPT(longest Processing Time)算法
LPT算法是在上面的贪心算法基础之上,先对\(n\)个任务按时间降序排序,然后再按照上面的贪心算法执行.

通过观察可以得出,当任务数小于或等于机器数的时候,LRT算法就是最优解.这时候只需要把任务\(i\)分配给机器\(i\).
引理3:如果任务数多于机器数\(m\),有\(L^* \ge 2t_{m+1}\).
设前\(m+1\)个任务的运行时间分别为\(t_1,\dots,t_{m+1}\),由于运行时间\(t_i\)是按照降序排列,所以前\(m+1\)个任务的运行时间都不小于\(t_{m +1}\),且由于鸽笼原则,至少有一个机器会被分配两个任务.
定理:LPT算法是Load Balancing的一个\(\frac{3}{2}\)近似算法.
证明:与证明贪心算法相同的方法 \[L_i=(L_i - t_j) + t_j \le L^* + \frac{1}{2}L^* = \frac{3}{2}L\]
那么LPT算法是Load Balancing的紧\(\frac{3}{2}\)倍近似算法吗?不是;LPT算法是Load Balancing的紧\(\frac{4}{3}\)倍近似算法吗?很可能是.
Centrer Selection Problem(中心选址问题)
定义:给定一个大小为\(n\)个地址集合\(s_1,s_2,\dots,s_n\)以及一个整数\(k>0\),选择\(k\)个中心使所有地址到离它最近的中心距离的最大值最短.

几个概念:
- \(dist(x, y)\):\(x,y\)的距离.
- \(dist(s_i, C)=\min\limits_{c \in C}\):\(s_i\)到离它最近的中心的距离,这里采用欧式距离.
- \(r(C)=\max\limits_{i} dist(s_i,C)\):最小的覆盖半径.
中心选址问题的目标便是找到一个中心集合\(C\)使覆盖半径\(r(C)\)最小,其中中心的数量等于\(k\).
距离的一些性质: \[dist(x,x)=0 \tag{同一性}\] \[dist(x,y)=dist(y,x) \tag{对称性}\] \[dist(x,y) \le dist(x,z) + dist(z,y) \tag{三角不等式}\]
贪心算法
开始时我们任意选取一个地址作为中心,接着选择离第一个中心最远的那个地址作为第二个中心,如此的重复进行,直到选了\(k\)个中心为止。

定理:贪心算法是中心选址问题的2倍近似解
证明(反证法):
假设\(r(C^*)<\frac{1}{2}r(C)\)
- 对近似解集合\(C\)的中心\(c_i\),总有一个最优解的中心\(c_i^*\)在\(c_i\)的圆中(任意一个最优解的中心\(c_i^*\)的圆里最少有一个地址\(s\),而贪心算法选址都是在地址集合中选的,并且\(c_i\)的半径 \(>\) \(c_i^*\)的半径,所以\(c_i^*\)必然在某一个中心\(c_i\)的圆里)
- 令\(c_i\)是与\(c_i^*\)对应的中心
- 对于任意一个离最优解\(c_i^*\)最近的地址\(s\),有
\[dist(s,C) \le dist(s, c_i) \le dist(s, c_i^*) + dist(c_i^*, c_i) \le r(C^*) + r(C^*) = 2r(C^*)\]
上式与假设\(r(C^*)<\frac{1}{2}r(C)\)相违背,故有\(r(C^*) \ge \frac{1}{2}r(C)\),即贪心算法是中心选址问题的2倍近似解。
中心选址问题有没有\(\frac{3}{2}\)倍近似解或者\(\frac{4}{3}\)倍近似解?
答:没有,除非P=NP,否则中心选址问题没有倍率比2小的近似算法。
Weighted Vertex Cover
带权值的顶点覆盖:对于给出的一个顶点带权值的图\(G\),找到一个顶点覆盖,使它们的权值之和最小。 (这里我们主要解决的是:求图\(G=(V,E)\)的顶点覆盖\(S\),要使顶点集合\(S\)中所有顶点的权值之和最小。
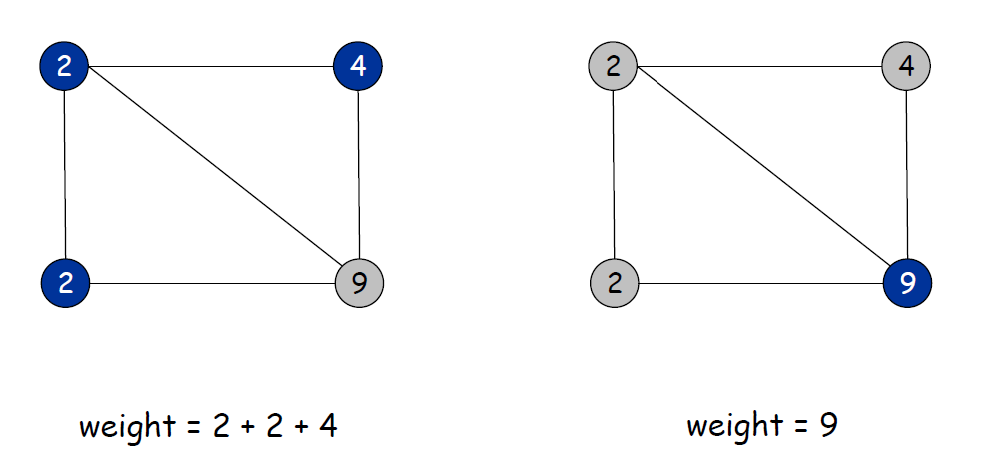
Pricing Method
定价法:因为顶点覆盖要求每条边至少有一个顶点在集合\(S\)里,每条边必须被一些顶点所覆盖,根据顶点\(i\)和\(j\),给边\(e = (i, j)\) 标上价格\(P_e\)。
公平性:与顶点\(i\)所连接的所有边的价格(权值)之和必须小于顶点\(i\)的权值。
引理::图\(G\)的所有边的价格(权值)之和 \(\le\) 顶点覆盖\(S\)中所有顶点的权值之和(两个简单的缩放)。
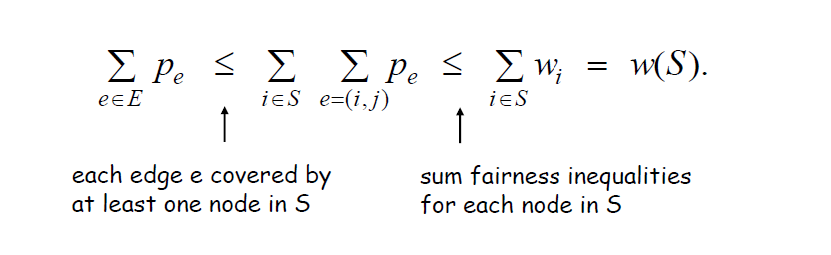
上面第一个\(\le\)不能写成等号,等号只在每条边都恰好只有一个顶点在\(S\)中时才成立,若有边的两个顶点都在\(S\)中,那么这条边就会被计算两次。
求解过程:边的价格设置与找寻顶点覆盖同时进行

例子:
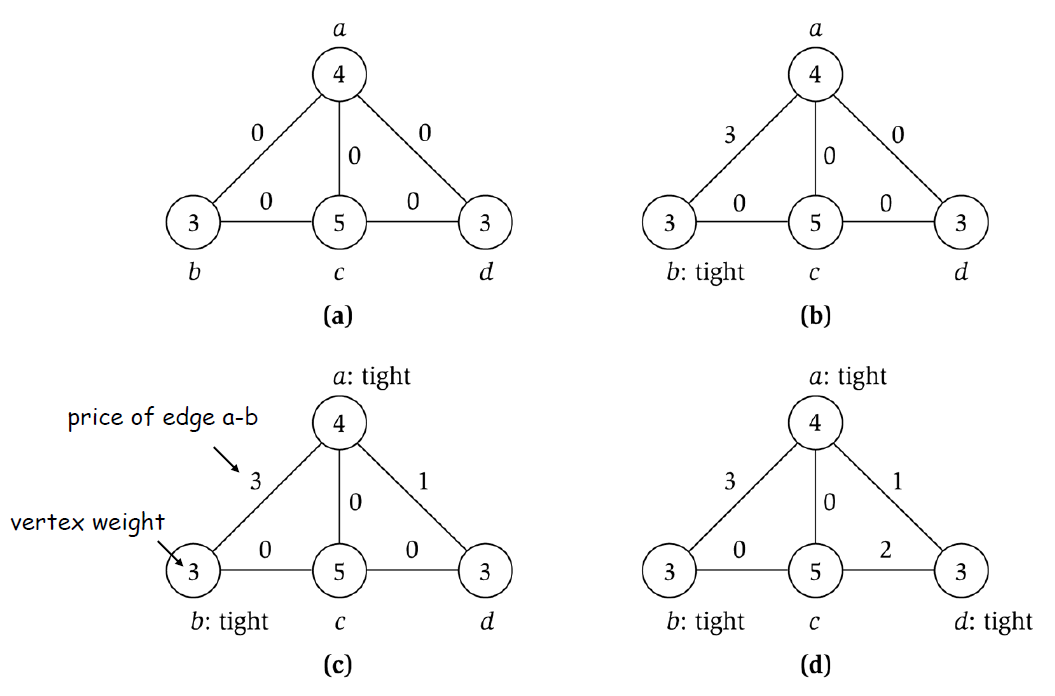
Pricing Method是Weighted Vertex Cover的一个2倍近似算法。
证明:
首先证明\(S\)是一个点覆盖:
算法结束条件:在while循环的每次迭代结束之后,至少有一个顶点会是紧致的(除非图没有边),所以在算法结束的时候每条边的两个顶点中至少有一个是紧的,即每条边至少有一个顶点在\(S\)中,而Vertex Cover要求每条边至少有一个顶点在\(S\)中,所以\(S\)必然是一个点覆盖,否则循环就不会停止。
然后再证明\(S\)是最优解的一个2倍近似解:
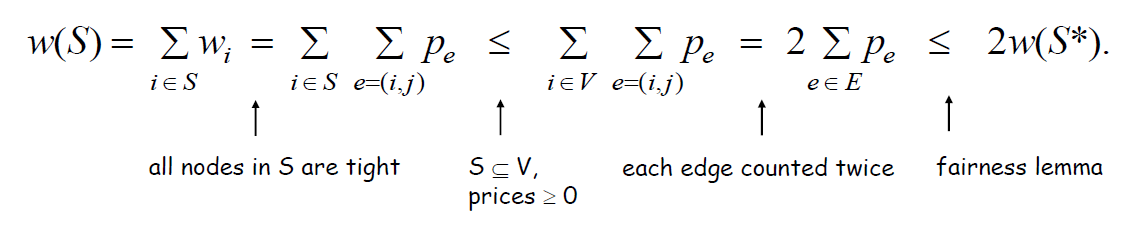
第一处放缩很容易得出,\(S\)肯定为顶点集\(V\)的一个子集;\(\sum\limits_{i \in V} \sum\limits_{e=(i,j)} p_e = 2 \sum\limits_{e \in E} p_e\)是因为计算与\(V\)中所有顶点相连的边时,每条边会被计算两次;最右边一个放缩为引理的结论。
线性规划解决最小带权点覆盖问题
整数规划
对于图\(G=(V,E)\),对图中的每个点\(v \in V\),定义函数\(x(v) \in {0, 1}\),且 \(x(v)=0\),表示顶点 \(v\)不在点覆盖集合里。
对图中任意一条边 \((u,v) \in E\),由点覆盖定义,顶点\(u\)、顶点\(v\) 至少有一个必须在点覆盖中 ,因此:\(x(u) + x(v) \ge 1\).
因而得到最小权值点覆盖的规划模型:其中\(w(v)\) 表示顶点\(v\)的权值。
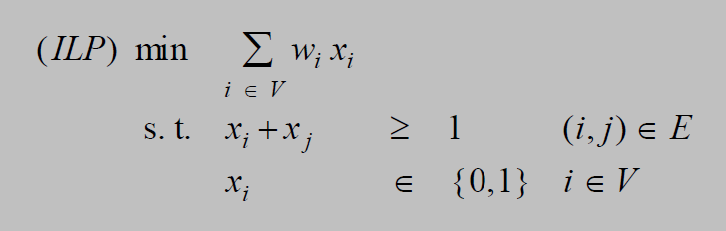
线性规划
线性规划在整数规划的基础之上不再限定\(x(v)\)只为0或1,而是有一个范围 \(x(v) \in [0, 1]\) 这样在整数规划中的\(x(u) + x(v) \ge 1\)仍然成立. 这是可以的。因为:前者是后者的一个特例。前者称为0-1整数规划,后者为普通的线性规划。因此,线性规划中的最优解是0-1整数规划最优解的一个下界(因为线性规划最优解包含了0-1整数规划最优解)。
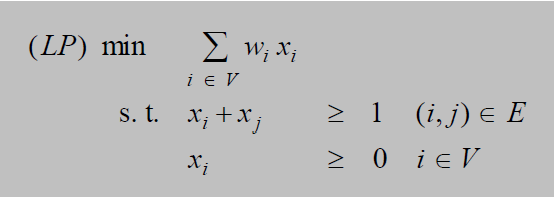
用线性规划的解来构造最小权值点覆盖问题的近似解算法:
对于每一个顶点\(v\),都会求得一个\(x(v)\)的值。若,\(x(v) \ge 1/2\) ,则将该顶点加入到点覆盖集合中,否则舍去顶点\(v\),直至图G中所有的顶点都处理完毕。此时得到的顶点集合\(C\)即为最小权值点覆盖问题的近似解的点覆盖集合。
线性规划求得的顶点集合C是最小权值点覆盖问题的二倍近似解:
设 \(C^*\) 是最小权值点覆盖问题的一个最优解,\(Z\) 是线性规划的一个最优解, \(C\)是最小权值点覆盖问题的近似解.
- 由于最小权值点覆盖问题的一个最优解是线性规划的一个可行解,故:\(Z \le W(C^*)\)(\(W\)为求权值的函数)
- 为什么求得的集合\(C\)就是一个点覆盖呢?因为对任意边\((u,v) \in E\),有\(x(u)+x(v)\ge 1\),即在\(x(u)\)和\(x(v)\)中至少有一个的值大于1/2。因此,顶点\(u\)、\(v\) 至少有一个会被加入到集合\(C\)中,从而使得图\(G\)中的每一条边都会被覆盖。
- 由下式
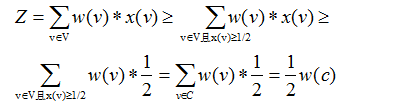
以及\(Z \le W(C^*)\),知:\(W(C) \le 2Z <=2W(C^*)\),即近似解\(C\)的权值\(W(C) \le\) 二倍最优解\(C^*\)的权值.
那么是否有比2倍近似解更小的近似解?最小的近似解倍率是多少?
答:有.
定理: 若 P \(\ne\) NP,那么没有比\(\rho = 1.3607(10\sqrt{5} - 21)\)更小的\(\rho\)-近似解.
多项式时间逼近算法(Polynomial Time Approximation Scheme)
上面的\(\rho\)-近似算法是通过牺牲最优解来换取时间和例子,多项式时间逼近算法可以产生任意高质量的解决方案,但以精度换取时间。
以背包问题为例:物品\(i\)的价值为\(v_i\) ,重量为\(w_i\);背包最多可以拿的物品重量为\(W\).现在求最大可以拿取的物品价值。
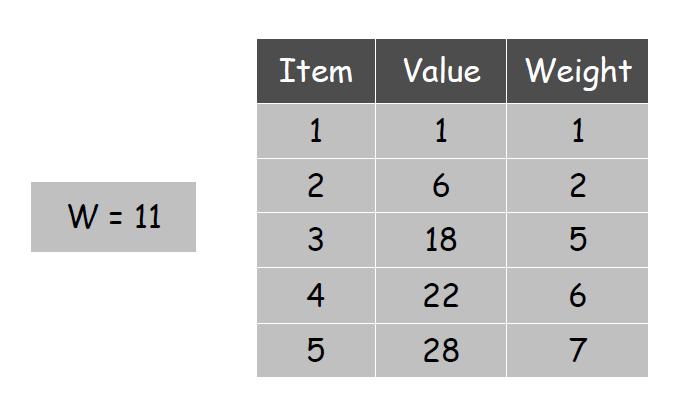
方法1:动态规划-1
定义\(OPT(i,w)=\)所有物品中可以拿到的最大价值。
- 若\(OPT\)没有选择物品\(i\)
- \(OPT\)在容量为\(w\)的情况下在物品\(1,2,\dots,i-1\)中选取得到最优解
- 若\(OPT\)选择物品\(i\)
- 新的容量为\(w-w_i\)
- \(OPT\)在容量为\(w-w_i\)的情况下在物品\(1,2,\dots,i-1\)中选取得到最优解

运行时间:\(O(n W)\)
- \(W=\)重量限制
- 输入不是多项式的
方法2:动态规划2
定义\(OPT(i,v)=\)物品\(1,2,\dots,i\)中拿取且得到的物品价值为\(v\)所消耗的最小重量
- 若\(OPT\)没有选择物品\(i\)
- \(OPT\)在物品\(1,2,\dots,i-1\)中选取得到的物品价值为\(v\)
- 若\(OPT\)选择物品\(i\)
- 消耗重量\(w_i\),且新的价值为\(v-v_i\)
- \(OPT\)在物品\(1,2,\dots,i-1\)中选取得到的物品价值为\(v\)
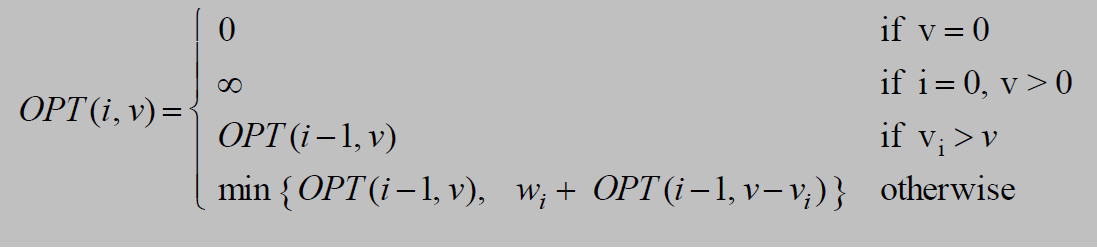
运行时间:\(O(n V^*)=O(n^2 v_{max})\)
- \(V^*\)为在\(OPT(n, v) \le W\)的情况下可以选取的最大价值
- 输入不是多项式的
多项式时间逼近算法
以上的动态规划都可以得到最优解,但是考虑一个问题:若所有物品的价值远大于重量的时候,上面的动态规划还可行吗?
这时候问题的输入不是多项式的(物品的价值,因为在计算机内数据都要转化为2进制再处理),这时候为了使求解时间更快,引入了新的算法多项式时间逼近算法(Polynomial Time Approximation Scheme)。它的大致思想是:
- 将所有的价值向上舍入到一个较小的范围里
- 在向上舍入后的实力上运行动态规划算法
- 得到向上舍入实例的最优解
注:这里一定要是向上舍入而不能是四舍五入,虽然全部向上舍入可能会在原来的问题中丢失一些较为优质的解,但是若四舍五入的时候,若有向下舍去的价值,可能在新的实例中找到的解在原问题中是不可行解。
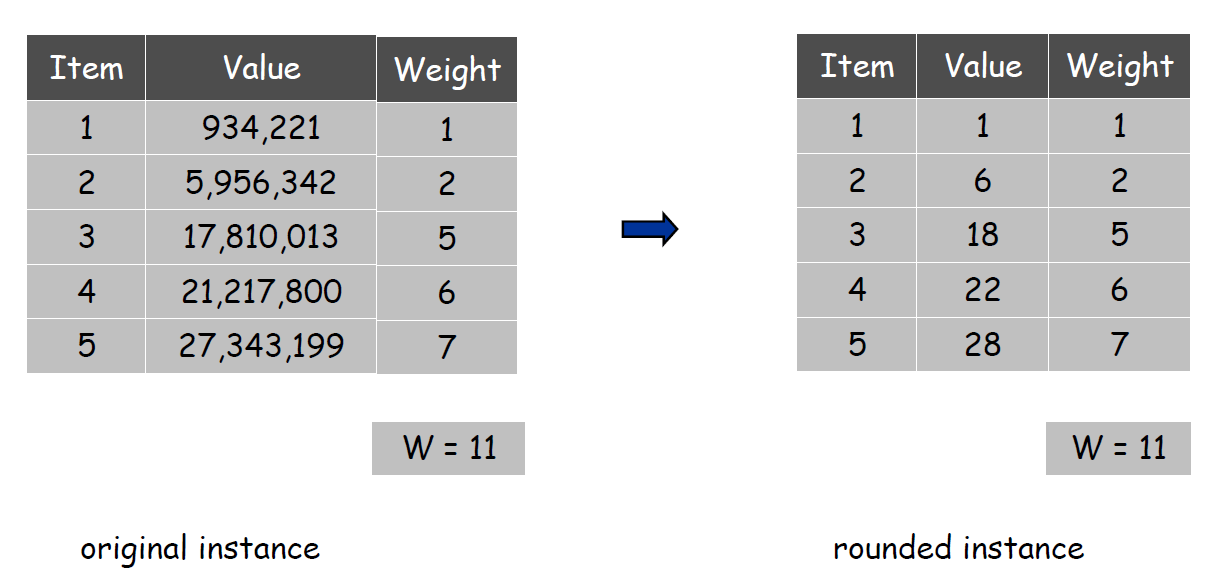
首先对所有价值向上舍入:
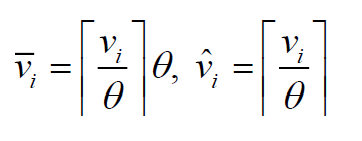
- \(v_{max}\)为原始例子里的最大价值
- \(\varepsilon\)为精确参数
- \(\theta\)为放缩因子
对于放缩之后的例子,复杂度\(O(n^3 / \varepsilon)\),使用上面的动态规划-2方法的运行时间为\(0(n^2 \hat{v}_{max})\).
其中
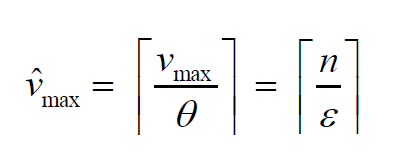
定理:若\(S\)为多项式时间逼近算法找到的一个解,同时\(S^*\)为另一个可行解,那么有 \((1+\varepsilon) \sum\limits_{i \in S}v_i \ge \sum\limits_{i \in S^*}v_i\)
证明:
