NP问题以及常见多项式规约

P、NP、NPC、NPH问题

P问题：存在多项式时间算法的决策问题。

NP问题 ：能在多项式时间内验证某个猜想答案的正确性，但问题求解可能在无法在多项式时间内完成。比如Composite问题、3-Satisfiability、Hamiltonian Cycle，很容易就确定一个答案是否正确，但确找不到一个公式来描述其规律。

结论1：P \(\subseteq\) NP

结论2：NP \(\subseteq\) EXP

EXP问题：存在指数时间算法的决策问题。

NPC问题: 需要满足两个条件

• 它是一个NP问题
• 所有的NP问题都可以规约到NP-complete

定理：若Y是一个NPC问题，那么Y可以在多项式时间内求解当且仅当P\(=\)NP

证明：

\(\Rightarrow\)

若P \(=\) NP，那么Y可以在多项式时间求解，因为Y是NP（NPC的第一个条件：它要先是一个NP）

\(\Leftarrow\)

若Y可以在多项式时间求解： - 令X为任意一个NP问题，因为X \(\le_p\) Y，而Y可以在多项式时间求解，故X也可以在多项式时间求解。NP \(\subseteq\) P - 又已知P \(\subseteq\) NP,所以 P \(=\) NP

如果我们给NPC问题找到了一个多项式时间复杂度的算法，那么也就意味着我们给所有的NP问题找到了多项式时间复杂度的算法，从而NP=P，因为P=NP，所以“P对NP问题”就可以被解决。但给NPC问题找一个多项式时间复杂度的算法太难了，所以现在人们普遍相信P≠NP。

NPH问题 ：满足上面NPC问题的第二个条件，但不一定要满足第一个条件，所以NPH的范围比HPC更大。

证明一个问题是NPC问题的步骤

• 证明这个问题Y属于NP
• 选择一个NPC问题X
• 证明X可以多项式规约到Y

证明一个问题是NPH问题的步骤

要证明一个问题是NP-hard，通常是找到一个已被证明了的NPC问题，并把这个NPC问题归约到该问题上去（即NPC \(\le\) NP-hard）,简单来说就是：

• 对问题A给定限制条件得到一个特例B问题
• 证明问题B是NPC问题

NPC之间规约的例子

3-SAT \(\le_p\) Independent Set

证明：给定一个3-SAT的例子\(\Phi\),可以构造一个大小为\(k\)的Independent Set当且仅当式子\(\Phi\)是可满足的。

构造:

• 3-SAT中的每个Clause包含独立集里的三个顶点，其中每个Literal对应一个顶点
• 连接句子里的点连接形成三角形
• 连接不同Clause里每个Literal和它对应的非

如下图所示：

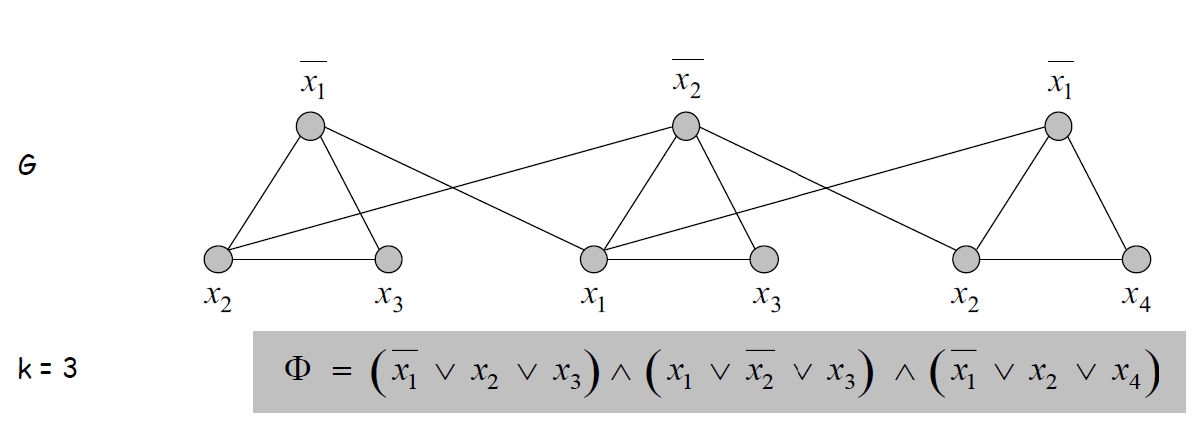
证明：

\(\Rightarrow\)

令S为一个大小为\(k\)的独立集，每个三角形里一定只有一个顶点在\(S\)里，设该顶点取1，其余顶点取0，则其肯定是一个满足3-SAT的赋值。

\(\Leftarrow\)

给定3-SAT一个满足的赋值，在每个三角形中选取一个取值为1的顶点，这样便构成了一个大小为\(k\)的独立集。

Hamiltonian Cycle problem

Hamiltonian Cycle:给定一个无向图 \(G=(V,E)\)，是否存在一个简单的环 \(\Gamma\) 包含 \(V\) 中所有的点。

有奇数个节点的Hamiltonian Cycle

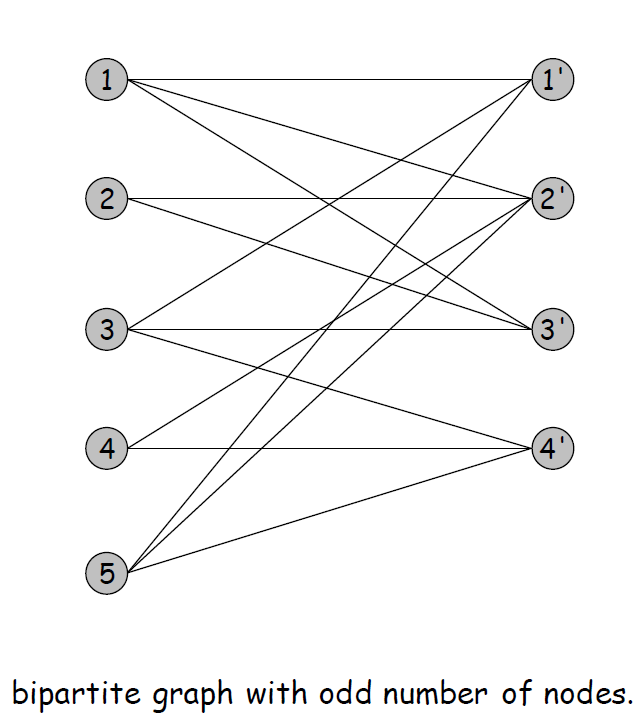
DIR-HAM-CYCLE：给定一个有向图 \(G=(V,E)\),是否存在一个简单环 \(\Gamma\) 包含\(V\)中所有顶点？

DIR-HAM-CYCL \(\le_p\) Ham-Cycle: 证明：给定一个有向图\(G=(V,E)\),构造一个有\(3n\)个节点的无向图\(G'\)，则\(G\)有Hamiltonian Cycle当且仅当\(G'\)有Hamiltonian Cycle。

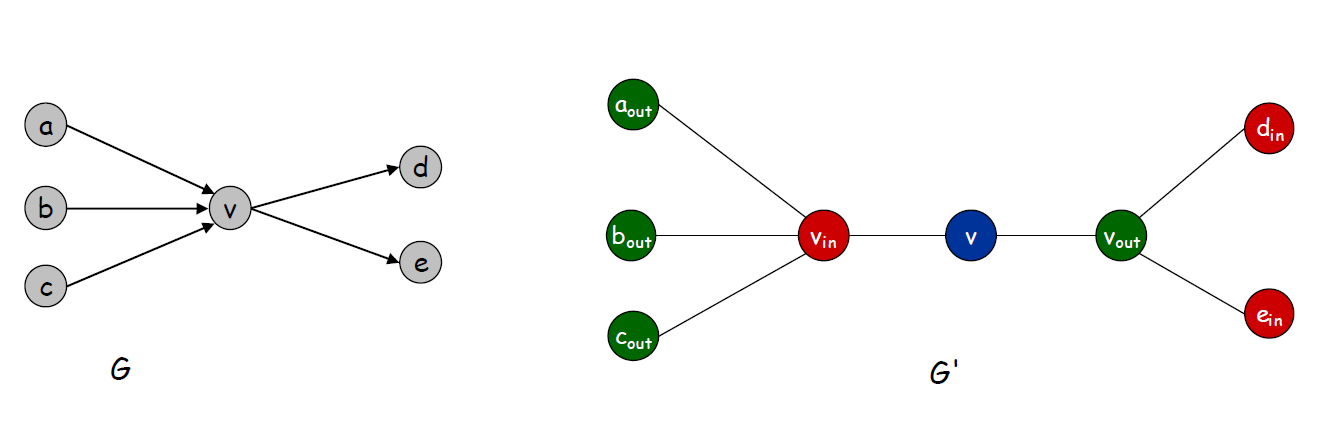
\(\Rightarrow\)

若\(G\)中有一个有向的Hamiltonian Cycle，则\(G'\)中肯定也有一个Hamiltonian Cycle，且顺序与有向图的节点顺序相同。

\(\Leftarrow\)

若\(G'\)中有一个无向的Hamiltonian Cycle，则从蓝色节点出发，节点的颜色出现顺序必然是两种中的一种 - B,G,R,B,G,R,\(\dots\) - B,R,G,B,R,G,\(\dots\)

若\(G'\)的Hamiltonian Cycle顺序是第一种，那么对应\(G\)中的Hamiltonian Cycle的节点顺序与其蓝色节点顺序相同；若\(G'\)的Hamiltonian Cycle顺序是第二种，那么对应\(G\)中的Hamiltonian Cycle的节点顺序与其蓝色节点顺序相反。

3SAT \(\le_p\) Hamiltonian Cycle problem

构造思路:有\(n\)个变量的3-SAT有\(2^n\)种可能的分配，要将其规约到Hamiltonian Cycle，其对应的Hamiltonian Cycle应该也有\(2^n\)种可能的分配方式。

构造方法：对一个有\(n\)个变量和\(k\)个句子的3-SAT,构造\(3k+3\)个节点的Hamiltonian Cycle，其中每个变量\(x_i\)对应\(3k+3\)个节点，令外再增加一个源点\(s\)、一个汇点\(t\)。

如果 \(x_i=1\)，则形成从左向右的一个路径；如果 \(x_i=0\)，则形成从右向左的一个路径。

对于每一个clause \(c_j=z_1 z_2 z_3\)，若\(z=x_i\),则添加有向边 \((v_{i,3j},c_j)和(c_j,v_{i,3j+1})\);若\(z=\bar{x}_i\),则添加有向边\((c_j,v_{i,3j})和(v_{i,3j+1},c_j)\)，这里\(1\le j\le m, 1\le i\le n\)。如上图所示（即若\(z=x_i\),该节点与\(c\)节点的连接顺序是从左边进入\(c\)节点，然后从右边出\(c\)节点；反之顺序相反）。

如果选择子句\(C_1\)中\(x_1=1\),则\(x_1\)对应的路径为从左向右;同理\(x_2=0\),则\(x_2\)对应的路径为从右向左；\(x_3=1\),则\(x_3\)对应的路径为从左向右。其余句子同理，这样就得到了最终的图\(G\)。

证明:

\(\Rightarrow\)

假设3-SAT有一个可满足的分配\(x^*\)：

• 对于\(x_i\),若其为1，则第\(i\)行从左往右遍历；反之，若其为0，则第\(i\)行从右往左遍历
• 且对于每个句子节点\(c_i\)，至少会有一行便利的时候会经过\(c_i\)，否则便不满足每个句子都为真的条件，也就是该分配并不是可满足的。

\(\Leftarrow\)

假设构造的图\(G\)有一个Ham-Cycle，那么

• 若Ham-Cycle进入句子节点\(c_i\)，那么它一定会返回相同的行，否则便不存在简单环。
• 这样Ham-Cycle里的句子节点\(c_i\)与同一行的两个相邻节点相连，记这两个相邻节点之间的边为\(e_i\)
• 去掉句子节点\(c_i\)，同时用\(e_i\)替换与\(c_i\)相连的两条边。
• 按上面的方法去掉所有的句子节点得到图也必然存在Ham-Cycle，且节点的顺序是相同的。
• 若Ham-Cycle的第\(i\)行是从左往右遍历的，便令\(x_i=1\);反之则令\(x_i=0\)，这样便得到一个分配方案，且其是可满足的。

这样便得到一个分配方式，且每个句子都是可满足的。

HAM-CYCLE \(\le_p\) TSP(Traveling Saleperson Problem)

TSP(Traveling Saleperson Problem)：给定一个\(n\)个城市的集合以及城市之间的距离\(d(u,v)\),是否存在一个旅行的路线使行走的距离\(\le n\)?

旅行者问题与HAM-CYCLE的区别在于：旅行者问题并不限定简单路径，也就是说一个节点可以通过多次，只需要考虑最后的路径长度。

DIR-HAM-CYCLE：给定一个有向图 \(G=(V,E)\),是否存在一个简单环 \(\Gamma\) 包含\(V\)中所有顶点？

$HAM-CYCLE \(\le_p\) TSP(Traveling Saleperson Problem)$

构造：给定一个HAM-CYCLE的实例\(G=(V,E)\),\(V\)中的每个节点构造一个城市节点，城市之间的距离根据\(E\)进行赋值: \[d(u,v)= \begin{cases} 1, (u,v) \in E \\ 2, (u,v) \notin E \end{cases}\]

则TSP中有一个旅行路径\(\le n\)当且仅当\(G\)中存在HAM-CYCLE

3-SAT \(\le_p\) 3-Colorable

3-Colorable:给定一个无向图\(G\)，并给图中的每个节点染上红、蓝、绿的其中一种颜色，那么是否存在一种染色方式使相邻的节点都有不同的颜色？

3-SAT \(\le_p\) 3-Colorable

构造：

• 对每个Literal，构造一个节点
• 同时添加三个节点\(T、F、B\)，连接这三个节点形成一个三角形
• 对每个literal节点，创建一个它的"非"并与它相连
• 所有的Literal节点都与\(B\)相连

如下图所示：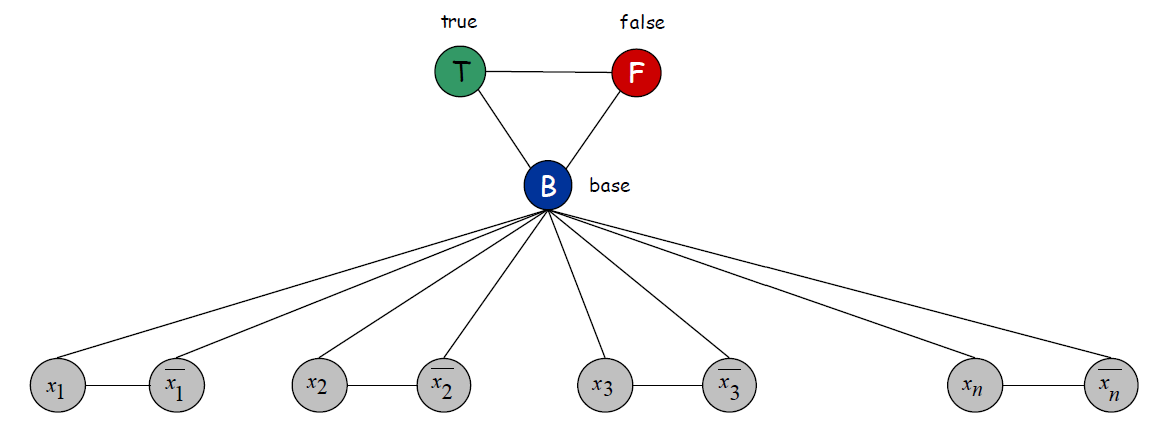

这样构造保证了下面的每个Literal节点都是绿色或红色，且它的“非”与它的颜色刚好相反。

继续接上面：

• 对每个Clause，假设\(C_i=x_1 \vee \overline{x_2} \vee x_3\),则对\(x_1 , \overline{x_2} , x_3\)添加6个节点以及13条边

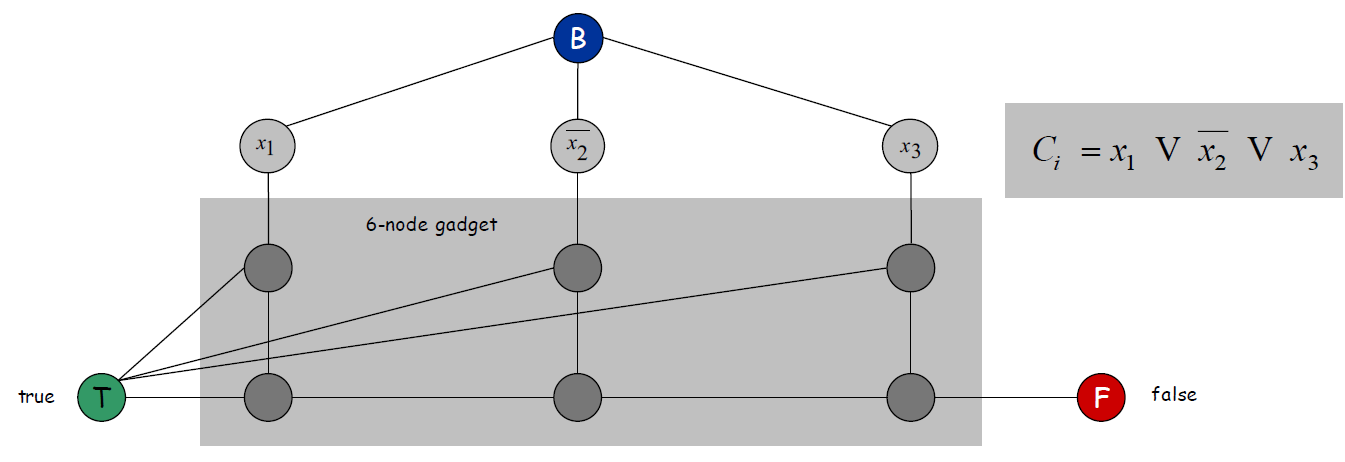
即\(x_1 , \overline{x_2} , x_3\)下方的两行一共6个节点，并将左下角的节点、第一行的节点与之前构造的\(T\)节点相连，右下角的节点与之前的\(F\)节点相连。

这样构造是为了保证当三个Literal节点全为红色的时候，是不满足三着色的，如下图所示：当三个Literal节点全为红色的时候，他们下面那行节点必须为蓝色，这样最后一行从左到右着色，最后一个节点冲突。

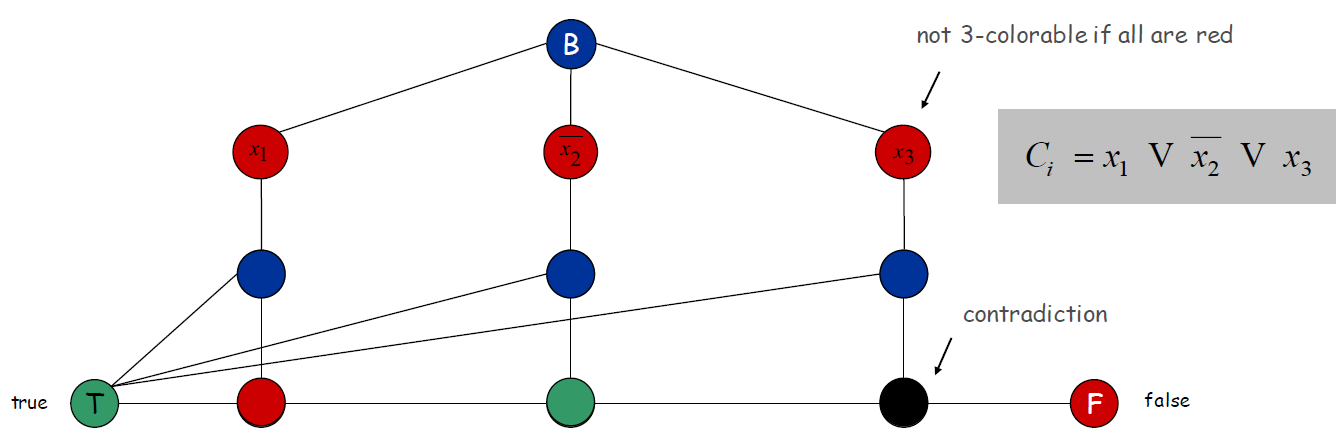
3-SAT \(\le_p\) 3-Colorable：

\(\Rightarrow\)

若图3-Colorable：

• 将所有为绿色的Literal节点设为真
• 由上面可知，当图3-Colorable的时候三个Literal节点至少有一个是绿色的，那么该句子的输出为真

\(\Leftarrow\)

若3-SAT是可满足的：则 - 三个Literal节点至少有一个为真 - 将为真的Literal节点染为绿色，然后将该节点下面的节点染为红色（否则会冲突），再继续将下面的节点染为蓝色 - 对中间一行没有染红的节点染为蓝色，然后它们下面一行没有染色的节点可唯一确定颜色

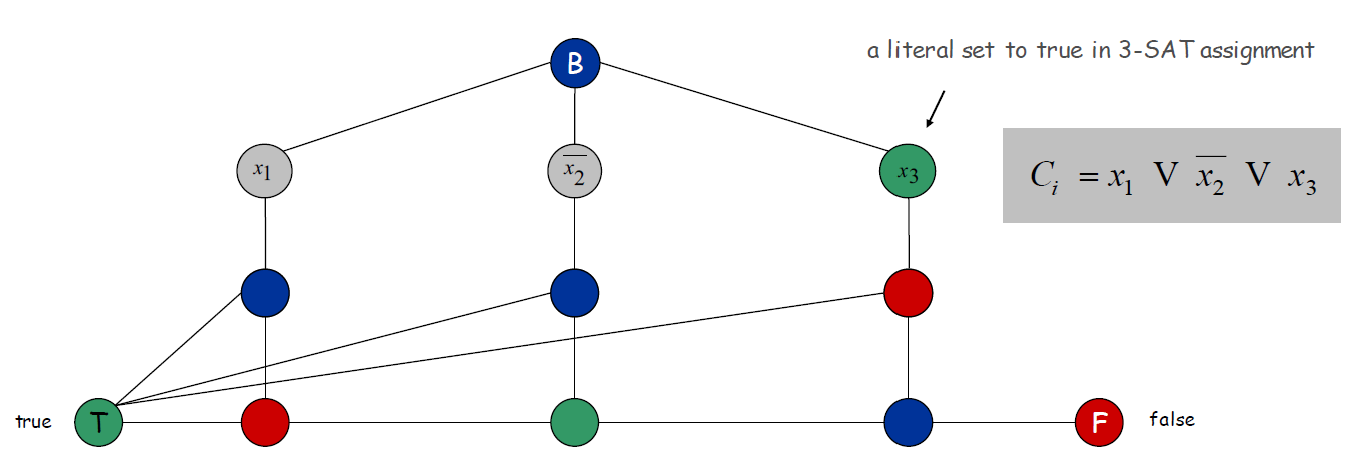
上面没有染色的Literal节点绿色、红色皆可。

3-COLOR搜索问题 \(\le_p\) 3-COLOR判断问题（自规约）

方法1：

将3-COLOR图中不相邻的点合并，合并后的点表示之前所有合并过来点的集合，如下图所示：

然后一直重复上述步骤，若图可以进行3着色，那么到最后图必然会合并为一个三角形。染色是对最后的三角形三个点所代表的点的集合染成不同的颜色，便为最后的3着色。

方法2：

设判定算法为\(D\)

1. 调用算法\(D\)判断原图是否有解，若无解，则返回NO。
2. 任意选择一对边\((u,v)\)，满足\((u,v) \notin E\)
   1. 考虑图\(G' = G + (u,v)\)，调用\(D\)判断是否有解。
   2. 若\(G'\)无解，标记点对\((u,v)\)；若有解，添加边\((u,v)\)到\(G\)中。
3. 返回步骤2，继续选择一对未标记点对。
4. 若图\(G\)构成一个三部完全图，每一部选择一个颜色，输出颜色方案。 ### 点覆盖搜索问题 \(\le_p\) 点覆盖判断问题

• 从1开始，依次查找该图有没有\(k^*\)个顶点的顶点覆盖(这样得到的第一次满足的\(k^*\) 的值就是该图最小顶点覆盖的数目)
• 从图中选出一个点\(v\) ，若去除该点后图的顶点覆盖数目变为\(k^* − 1\)，则\(v\)是原图顶点覆盖中的一员，反之则不是
• 在\(G − v\)中递归执行上述两步。

Ham-Cycle搜索问题 \(\le_p\) Ham-Cycle判断问题

证明：若可以在多项式时间内给出判定一个图是否存在哈密尔顿圈，则可以在多项式时间内找到一个图的哈密尔顿圈（如果存在的话）

首先判断\(G\)中是否存在Ham-Cycle,若不存在则算法结束，如果存在则继续寻找Ham-Cycle:

对G中的每条边e
{
    若G-e不存在Ham-Cycle，将e加入S中；
    否则令G=G-e
}
最后所得的集合便是一个Ham-Cycle