最大流最小割
最小割
在图论中,去掉其中所有边能使一张网络流图不再连通(即分成两个子图)的边集称为图的割。一个$ st-cut $即去掉的边把源点s和汇点t划分在两个不同的部分。
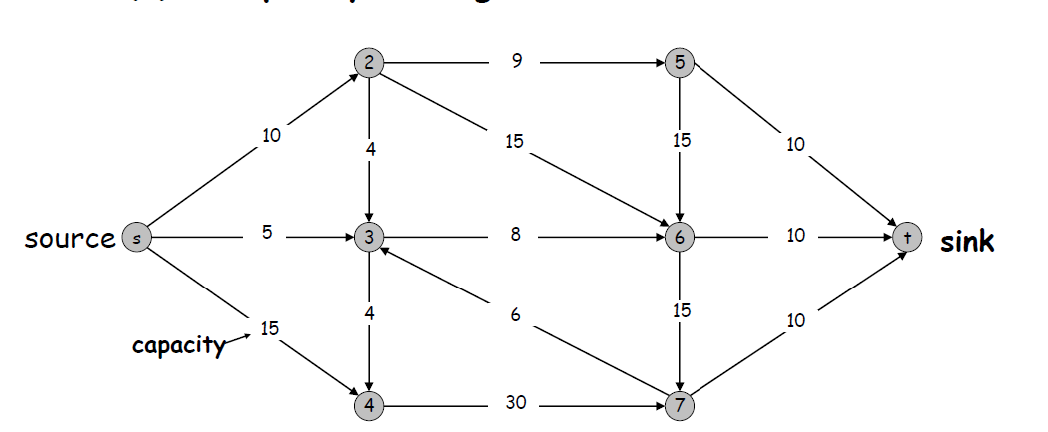
一般来说,一张图中有多个不同的\(st-cut\),如下图便为其中一个 \(st-cut\) 。
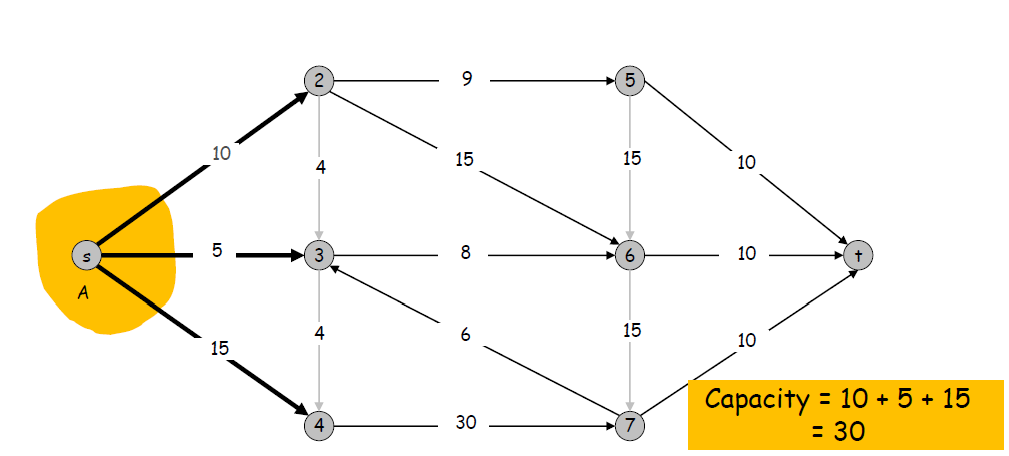
但是在实际应用中,我们去掉每条边往往都是有代价的,以边的容量作为权值,一个割中去掉的边的权值之和为这个割的值,那么最小割就是这张图上最小的割。
最大流
为了求解最小割,需要引入最大流的概念。用边的权值表示边的最大流量,一个 \(st-flow\) 是从源点s到汇点t的流量。通俗的讲,最大流就是从源点s到汇点t的最大流量。
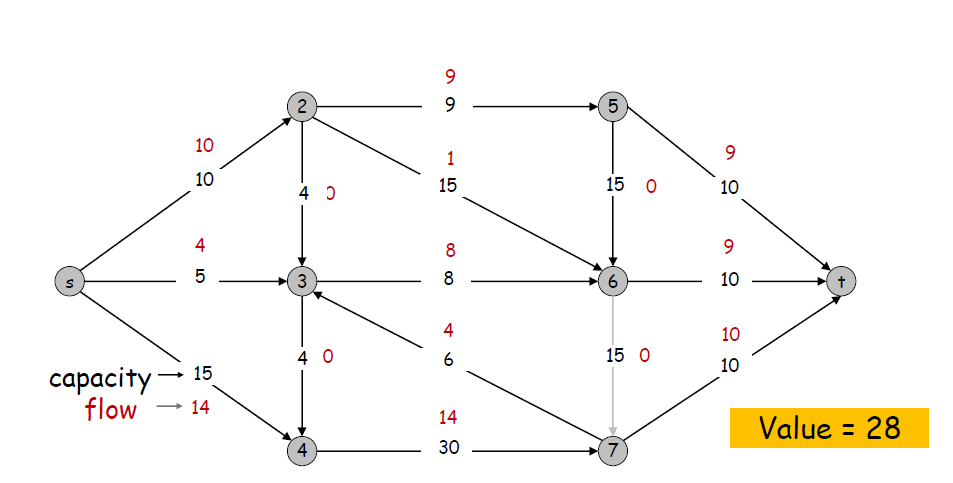
求解最大流
贪心算法
- 开始时对每条边e令\(f(e)=0\)
- 找到一条从源点s到汇点t的路径 \(s \rightarrow t\) 使路径上的每条边e满足 \(f(e)<c(e)\) ,其中 \(c(e)\) 为边e的权值
- \(flow = flow + 路径上的流量\)
- 重复上述步骤直至找不到新的路径
Ford-Fulkerson算法
残留图(Residual Graph)
在另一个图中,额外构造一个反向边,权值是实际流过该边的流量 \(f(e)\) 。
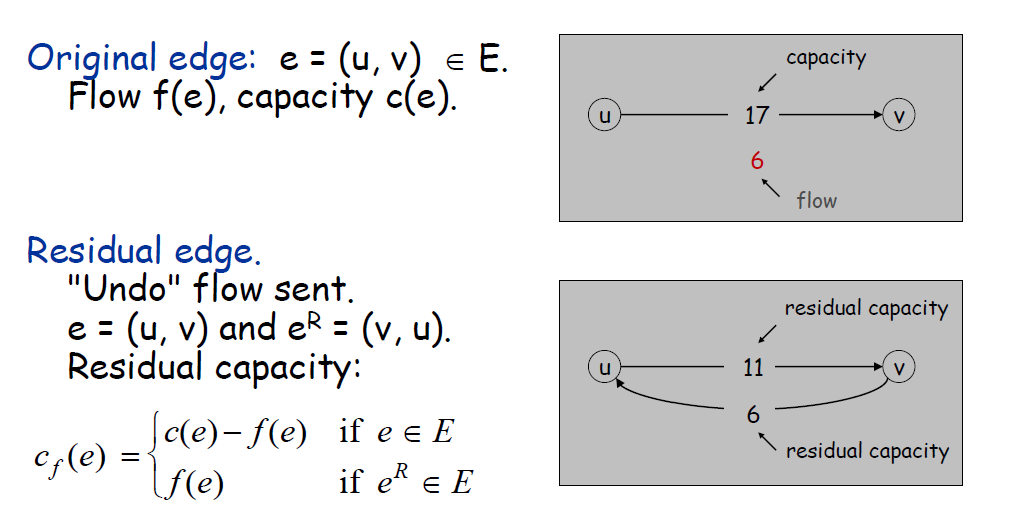
剩余图有以下性质: - 增广路径(Augmenting Path):一个增广路径P是从残余图中的一条简单路径 \(s \rightarrow t\) - 增广路径的容量是该条路径所有边中的最小权值
算法说明
- 每次找到一条从s到t的增广路径,并调整flow和残留图,不断调整直到没有增广路径
- 当残留图中不存在从s到t的增广路径时,该图已经达到最大流
例子
初始时没有反向边,此时残留图等于原图
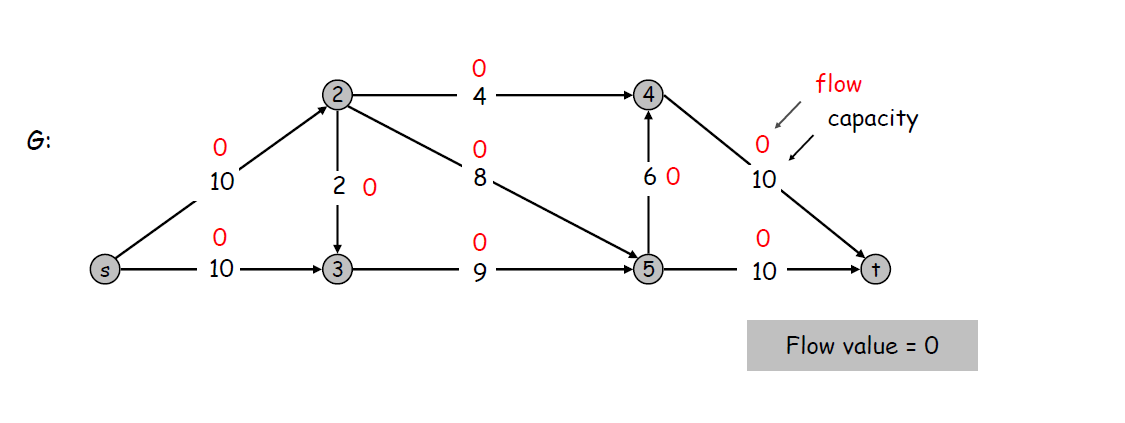
从中选取一条增广路径,并更新残留图和原图
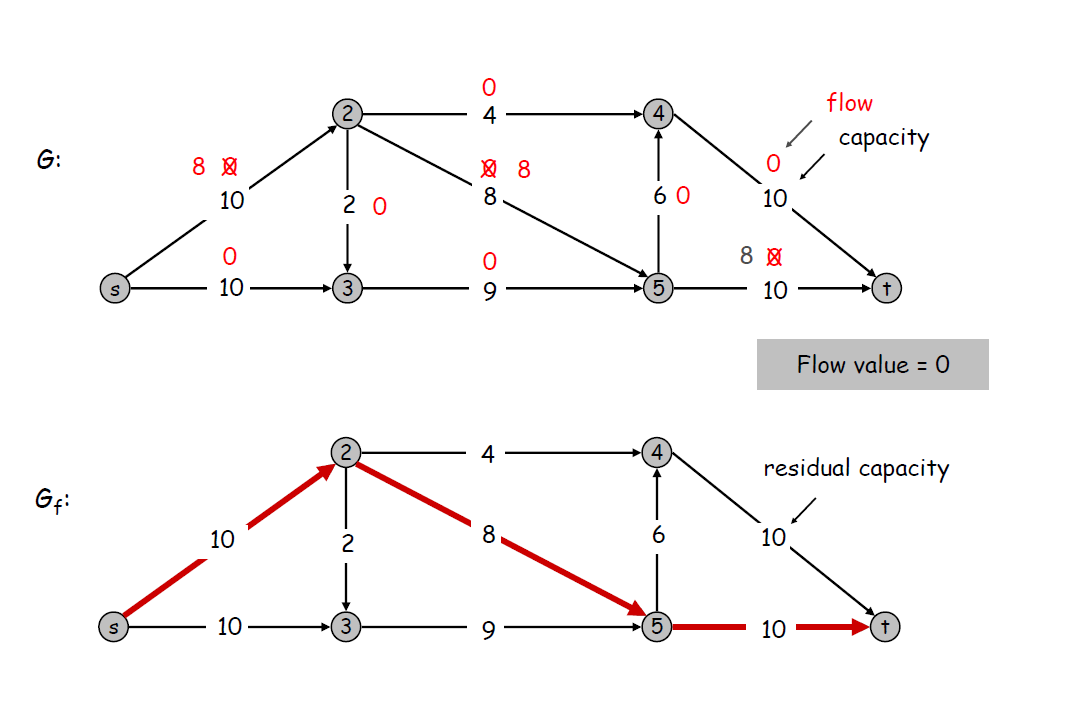
重复上面的步骤,注意增广路径一定要从残留图中找,且可以使用残留图中的反向边.
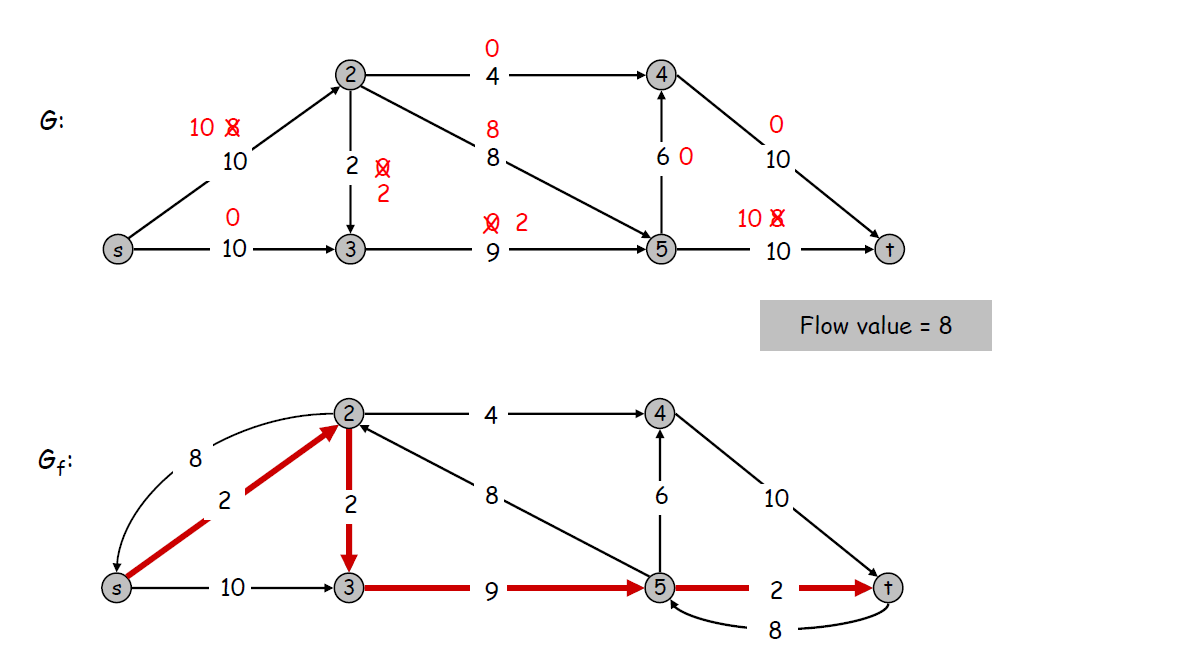
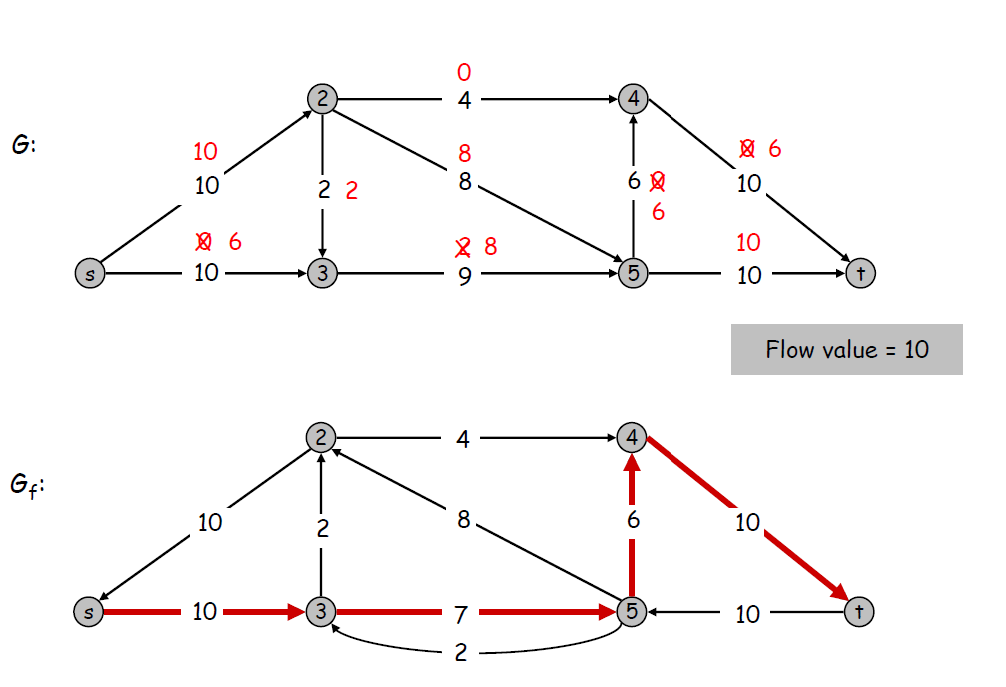
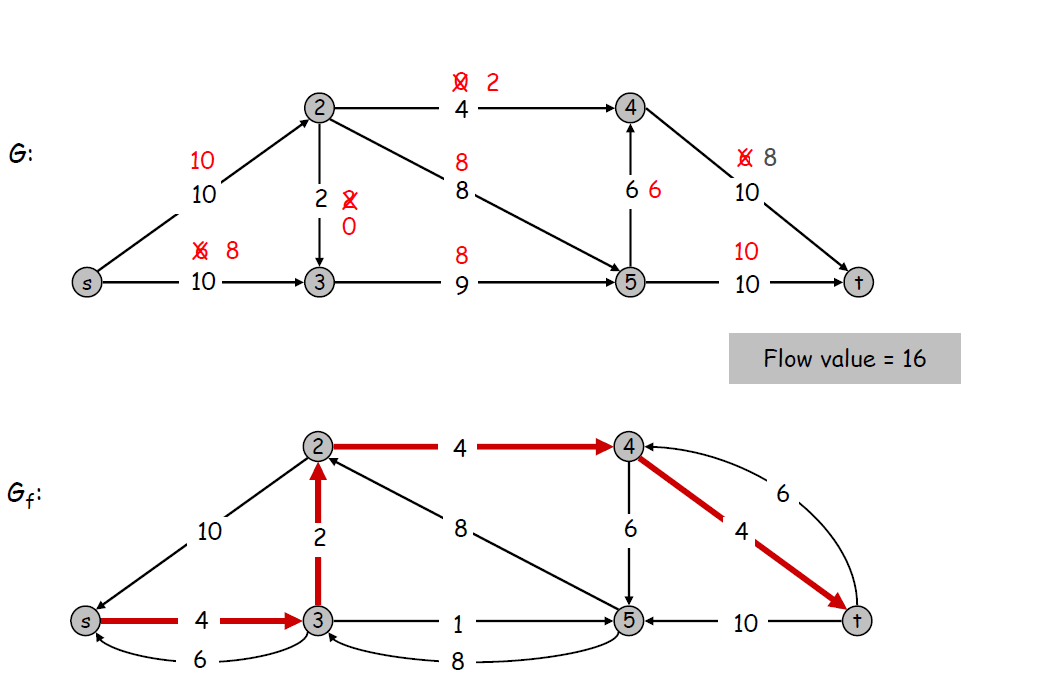
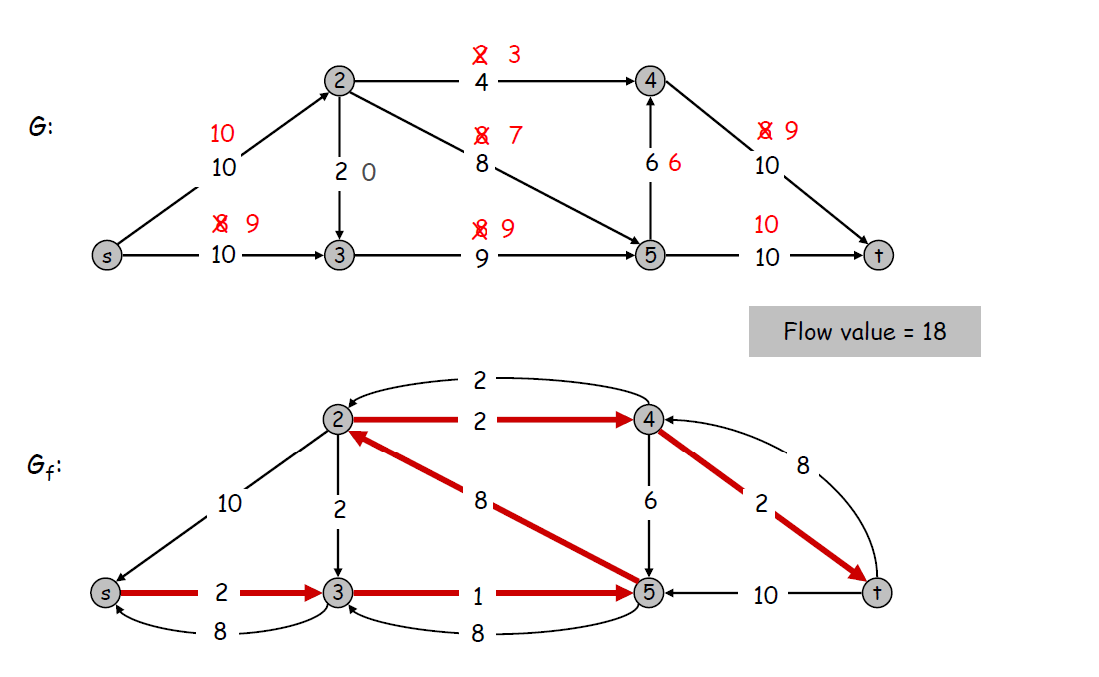
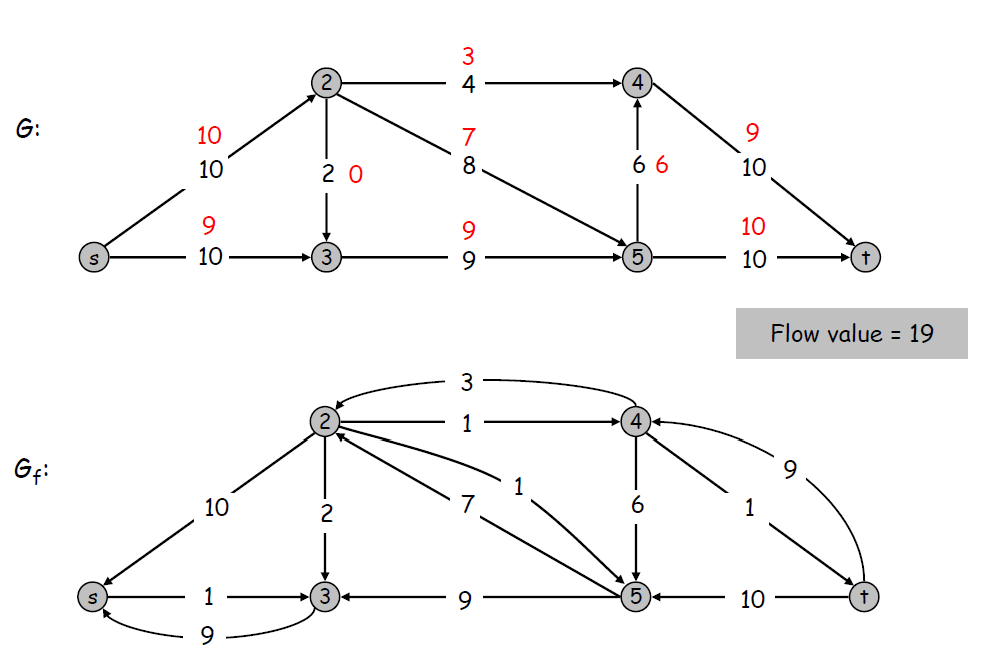
此时,没有新的增广路径,则最大流的值等于流进s的流量,即 \(flow = s_{in}\)
最大流与最小割的关系
最大流最小割定理:最大流=最小割。 最大流-最小割定理用来证明Ford-Fulkson方法的确达到了最大流.

证明:
- \((i) \Rightarrow (ii)\) :弱对偶性法则的推论
- \((ii) \Rightarrow (iii)\)
:反证法
若f是一个最大流,且仍存在增广路径,那么可以让f加上增广路径的流量,与f是一个最大流相悖.故\((ii) \Rightarrow (iii)\)成立 - \((iii) \Rightarrow (i)\)
设f是一个流,且没有增广路径,令A等于s的可达顶点集,则
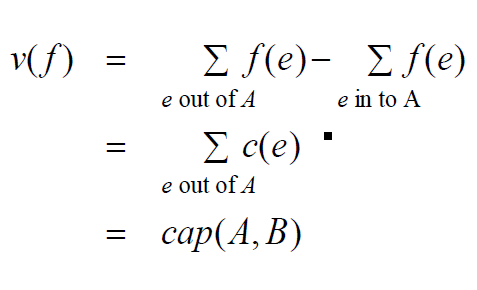
求出最大流之后如何求最小割
求完最大流之后,在残留图中用BFS遍历,结束后可得到一个从\(s\)出发可达的集合,将原图分为两个子集合,\(s\)可达的集合\(X\)以及\(s\)不可达的集合\(Y\),其中\(Y\)中必然包含汇点\(t\)。
连接两个集合\(X\)和\(Y\)的边有两种情况
- 已被占满的前向边
- 没有流量的反向边(即从\(Y\)到\(X\)的边)
其中被占满的前向边集合就是所求的最小割
还是用上面的例子 
在\(G_f\)中,用BFS遍历可得\(s\)可达的顶点集合为\(\{s, 3\}\),在\(G\)中查看\(\{s, 3\}\)与图中剩余顶点集合的关系。
- 已被占满的前向边:\(s \rightarrow 2, 3 \rightarrow 5\)
- 没有流量的反向边:\(2 \rightarrow 3\)
所以图中的一个最小割为\(s \rightarrow 2, 3 \rightarrow 5\)。