多项式规约
多项式规约
定义:若问题X 的任意实例可以由下面两条之和解决
- 问题X可以通过多项式时间的基本运算步骤转换为问题Y;
- 问题X多项式次调用求解问题Y的算法,且问题Y可以在多项式时间内被求解。
那么称问题X可以多项式规约到问题Y,记为 $ X _{p} Y $。需要注意的是,问题X转换为问题Y之后,问题Y的运行时间是建立在问题Y的输入上。
多项式规约的几个性质:
- 若 \(X \le_{p} Y\),则若Y能在多项式时间内求解,那么X也能在多项式时间内求解。
- 若 \(X \le_{p} Y\),则若X不能在多项式时间内求解,那么Y也不能在多项式时间内求解。
- 若 \(X \le_{p} Y\) 且 \(Y \le_{p} X\),那么X和Y是等价的。
基本的规约方法
- 简单的恒等归约:比如最大独立集和最小点覆盖。
- 从特殊例子到一般例子:比如 \(点覆盖
\le_{p} 集合覆盖\)。
- 通过一些小技巧规约。比如 \(3-SAT \le_{p} 独立集\)
简单的恒等规约
独立集问题(Independent Set)
定义:给定一个图 \(G=(V,E)\)和一个整数k(V为顶点集,E为边集),是否有一个V的子集 \(S \subseteq V\)使得 \(|S| \ge k\)并且图中每条边至多有一个顶点在S中?
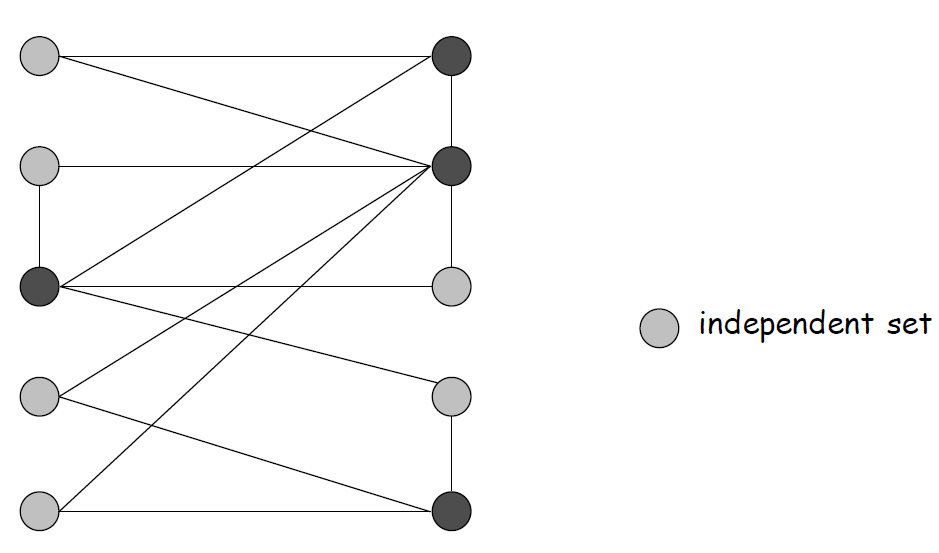
点覆盖问题(Vertex Cover)
定义:给定一个图 \(G=(V,E)\)和一个整数k,是否有一个V的子集 \(S \subseteq V\)使得 \(|S| \le k\)并且图中的每条边至少有一个顶点在\(S\)中?
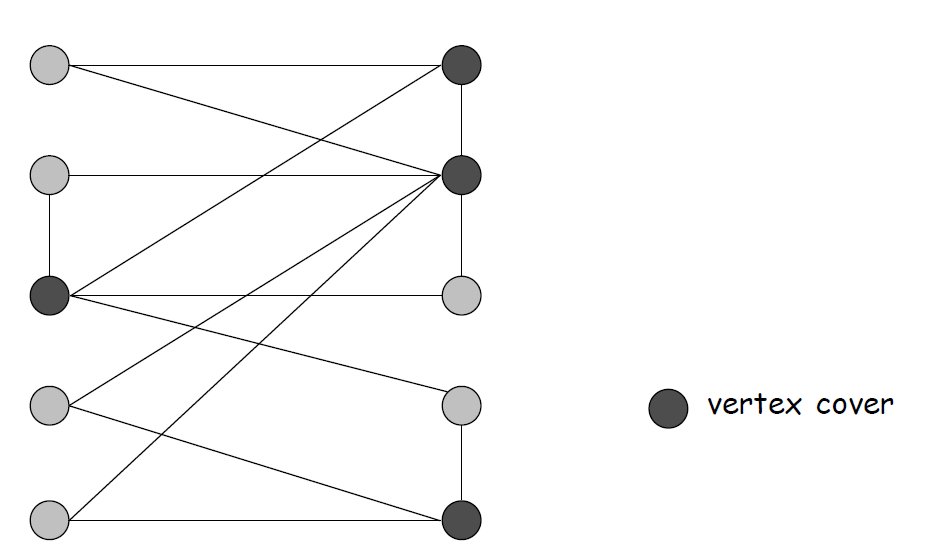
Vertex Cover和Independent Set的关系
定理: \(点覆盖 \equiv_p 独立集\)
证明如下:
\(\Rightarrow\)
- 令\(S\)为任意独立集
- 对任意的边 \((u,v)\)
- \(S\)是独立集 \(\Rightarrow\) \(u \notin S\) 或 \(v \notin S \Rightarrow u \in V - S\) 或 \(v \in V - S\)
- 所以 \(V-S\) 是一个点覆盖
\(\Leftarrow\)
- 令 \(V-S\)是一个点覆盖
- 对两个顶点 \(u \in S\) 及 \(v \in S\)
- 若 \(V-S\) 是一个点覆盖,那么 \((u, v) \notin E\)
- 因此,没有相邻的顶点在 \(S\) 中 \(\Rightarrow\) \(S\)是独立集
从特殊例子到一般例子
集合覆盖(Set Cover)
定义:给定一个集合\(U\),以及\(U\)的子集\(S_1,S_2,\dots,S_m\)以及一个整数\(k\),是否存在小于或等于\(k\)个子集\(S_i\)的并等于\(U\)?
例子:

Vertex Cover归约到Set Cover
证明:给定一个Vertex-Cover的实例\(G=(V,E),k\),可以构造一个与Vertex Cover大小相等的Set Cover的实例。(从特殊例子到一般例子)
- 创建一个Set Cover的实例\(k = k,U=E,S_v=\{e \in E: 与V相连的边\}\)
- 可以看到Set Cover的\(size \le k\)当且仅当Vertex Cover的\(size \le k\)
例子:有如下点覆盖
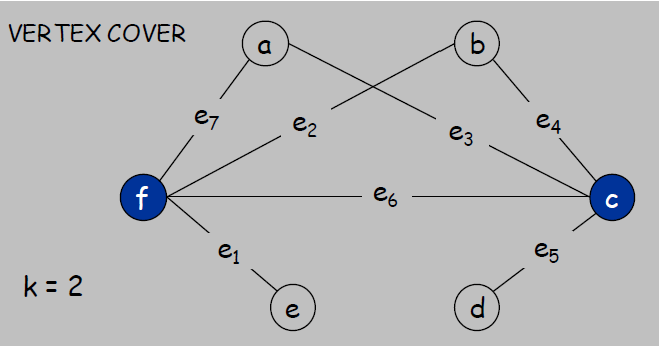
构造Set Cover的\(U\)为Vertex Cover的边集,即\(U=(1,2,3,4,5,6)\),Set Cover的每个子集\(S_i\)为Vertex Cover中对应顶点所连的边,故有 \[ S_a=\{3,7\}, \\ S_b=\{2,4\}, \\ S_c=\{3,4,5,6\}, \\ S_d=\{5\}, \\ S_e=\{1\}, \\ S_f=\{1,2,6,7\} \]
可以看到\(S_c\)和\(S_f\)构成一个Set Cover的实例,而这两个子集对应的顶点恰好组成一个Vertex Cover的实例。
通过"小技巧"规约
3-SAT问题
Literal(字):一个布尔变量或者它的非\(x_i \quad or \quad \overline{x_i}\)
Clause(句子):Literal的析取 \(C_j = x_1 \vee \overline{x_2} \vee x_3\)
Formula(式子):Clause的合取 \(\Phi=C_1 \wedge C_2 \wedge C_3 \wedge C_4\)
SAT:给定CNF式子\(\Phi\),是否存在一个满足结果是True的分配\(x_1,\dots,x_n\)?若有则称式子\(\Phi\)是可满足的。
3-SAT:每个Clause只有三个Literals。
例子:
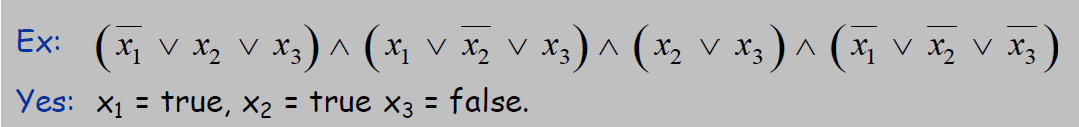
3-Satisfiability(3-SAT)归约到Independent Set
证明:给定一个3-SAT的例子\(\Phi\),可以构造一个大小为\(k\)的Independent Set当且仅当式子\(\Phi\)是可满足的。
构造: - 3-SAT中的每个Clause包含独立集里的三个顶点,其中每个Literal对应一个顶点 - 连接句子里的点连接形成三角形 - 连接不同Clause里每个Literal和它对应的非
如下图所示:
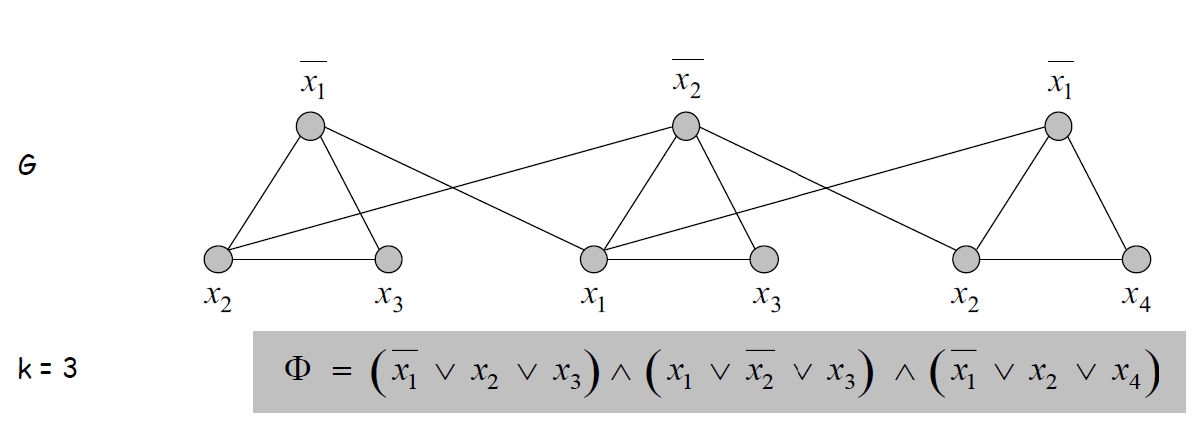
证明:
\(\Rightarrow\)
令S为一个大小为\(k\)的独立集,每个三角形里一定只有一个顶点在\(S\)里,设该顶点取1,其余顶点取0,则其肯定是一个满足3-SAT的赋值。
\(\Leftarrow\)
给定3-SAT一个满足的赋值,在每个三角形中选取一个取值为1的顶点,这样便构成了一个大小为\(k\)的独立集。
自规约(重要)
决策问题(Decision Problem):诸如"是否存在一个\(size \ge k\)的点覆盖"
求解问题(Search Problem):诸如"寻找一个最小的点覆盖"
自规约(Self-Reducibility):Search Problem \(\le_p\) Decision Problem