胜者树与败者树
胜者树与败者树是完全二叉树。就像是参加比赛一样,每个选手有不同的实力,两个选手PK,实力决定胜负,晋级下一轮,经过几轮之后,就能得到冠军。不同的是,胜者树的中间结点记录的是胜者的标号;而败者树的中间结点记录的败者的标号。 胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后,利用中间结点的信息,还是能够快速地找到最值。在k路归并排序中经常用到。
胜者树
胜者树的一个优点是,如果一个选手的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他比赛的结果。
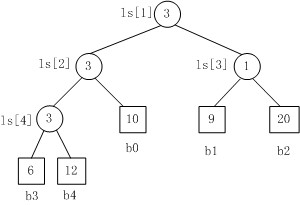
上图是一个胜者树的示例。规定数值小者胜。 1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3; 2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为3; 3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1; 4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为3。
取出胜者b3之后,叶子结点b3的值变为11时,重构的胜者树如下:
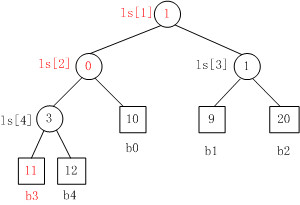
- b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
- b3 PK b0,b0胜b3负,内部结点ls[2]的值为0;
- b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
- b0 PK b1,b1胜b0负,内部结点ls[1]的值为1。
用胜者树对n个节点实现排序操作,构建胜者树和构建堆比较相似,区别在于胜者树只有叶子节点存放了数据,中间节点记录的是叶子节点间的关系。
胜者树在每次重构时只需与其兄弟结点比较,一直到根节点选出胜者为止。
败者树
败者树是胜者树的一种变体。在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
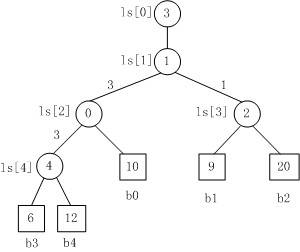
上图是一棵败者树。规定数大者败。
- b3 PK b4,b3胜b4负,内部结点ls[4]的值为4;
- b3 PK b0,b3胜b0负,内部结点ls[2]的值为0;
- b1 PK b2,b1胜b2负,内部结点ls[3]的值为2;
- b3 PK b1,b3胜b1负,内部结点ls[1]的值为1;
败者树重构过程如下: - 将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。 - 比赛沿着到根结点的路径不断进行,直到ls[1]处。把败者存放在结点ls[1]中,胜者存放在ls[0]中。
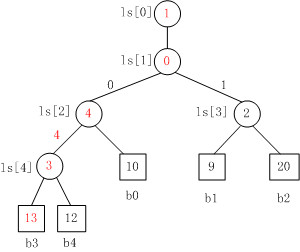
胜者树、败者树、堆比较
相同点
这三者空间和时间复杂度都是一样的。调整一次的时间复杂度都是O(logN)的。
不同点
一开始就是只有堆来完成多路归并的,但是人们发现堆每次取出最小值之后,把最后一个数放到堆顶,调整堆的时候,每次都要选出父结点的两个孩子节点的最小值,然后再用孩子结点的最小值和父节点进行比较,所以每调整一层需要比较两次。
这时人们想能否简化比较过程,这时就有了胜者树。这样每次比较只用跟自己的兄弟结点进行比较就好,所以用胜者树可以比堆少一半的比较次数。
而胜者树想要比较兄弟结点首先要获得其父结点,也就是说需要访存两次,这时人们又想能否再次减少比较次数,于是就有了败者树。败者树每个新元素上升时,只需要获得父节点并比较即可。
总的来说,败者树与胜者树相比减少了访存时间。现在程序的主要瓶颈在于访存了,计算倒几乎可以忽略不计了。